by Dan Hughes and Tomas Milanovic
Further reflections on the application of the divergence theorem to the Earth’s climate system.
Introduction
The subject of a recent post at CE was application of the divergence theorem to some aspects of Earth’s climate systems. Application of this theorem to an equation for conservation of the total energy of the atmosphere led to requirements for that energy to be constant. A corresponding post appeared at . . .aTTP not long after the CE post. The post at . . .aTTP was focused on disagreements with the post at CE.
These posts and associated lively discussions led to disagreements among the commenters on several mathematical aspects of the subject. The objective of the present post is to keep focus on some points of major disagreement: And hopefully, agreements.
A copy of the technical document that formed the basis of the previous post is available from here. That document has been updated and is available here.
Two of the issues for which there was massive disagreement were associated with the use of some well established concepts from mathematics and thermodynamics. In particular, known results and theorems from Partial Differential Equation (PDE) theory as well as from non-linear dynamics need to be strictly respected.
We directly address the points of major disagreement and have tightened our mathematical and thermodynamic arguments. The foundations of our agreements in mathematics and thermodynamics that were used in the previous post are further explained and expanded.
Divergence Theorem
The divergence theorem states that the oriented flux of a vector field through a closed surface is equal to the volume integral of the divergence over the region inside the surface.
Physically this theorem is used for different conservation laws (mass, energy, charge) which take the general form of continuity equation:

where q is the density of some quantity, J is a vector field representing the flow of this quantity and S are sources/sinks of this quantity. In the case of energy which can neither be created nor destroyed we have:
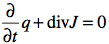
Integrating this equation over some volume V with boundary B and applying the divergence theorem we obtain the well known law that “The variation of energy in a volume V is equal to the oriented flux through its boundary B“.
Obviously if the continuity equation is written for non-conserved quantities like radiation or heat, it is necessary to take into account all sources and sinks of this quantity before integrating in the volume V .
Application of the theorem to idealized sub-systems of Earth’s climate system leads to equations for the time-rate-of-change of the total energy content of the sub-systems. The resulting equations must identify physical phenomena and processes that can lead to changes in energy content, and the locations of these. Modeling and evaluations of these will determine if the net flow of energy is positive of negative (as per the theorem), and thus determine the time-rate-of-change in total energy.
Importantly, the equations also lead to the requirements that must be met in order for the total energy content to remain constant.
It is also to be noted that when this theorem is applied to energy, the results state only the obvious – energy is conserved – but gives no information about the dynamics of the system.
The divergence theorem is also known as Gauss’s theorem, or Ostrogradsky’s theorem, or the Gauss-Ostrogradsky theorem, and finally Stokes’s theorem. Establishing historical precedent is sometimes a tricky, and long-term, process.
Earth’s Climate System and Equilibrium
There can be no question that Earth’s climate system is a system that operates far from equilibrium. Here we use equilibrium in the universally established and accepted sense that the word is used in thermodynamics. In thermodynamics, equilibrium means absence of all gradients: Nothing can change over time, and nothing can change in space.
Flows of mass, momentum, energy, chemical, and biological processes are present in Earth’s climate system, and these operate over very wide ranges of time scales. These flows require the existence of gradients in driving potentials. Gradients in driving potentials absolutely ensure that the system is never in equilibrium.
In the universally accepted sense of equilibrium, the gradients will exist for all time and Earth’s climate system will always be far from equilibrium. The flows change on all time and space scales, and these changes will affect, to lesser and greater extents, the radiative energy transport properties and characteristics of Earth’s climate.
When thermodynamics is the subject of discussions the universally accepted nomenclature should form the basis of word meanings. In this regard, Earth’s climate system cannot and will never attain an equilibrium state. More generally it must be noted that any rotating sphere exchanging radiation with a point-like source is never in equilibrium because different points on its surface are at different temperatures and therefore temperature gradients exist at all time.
Given the impossibility of attaining an equilibrium state, other possibilities for the state of Earth’s climate systems may only be; (1) unsteady state, (2) stationary state, or (3) steady state.
GCMs
The GCMs, and the evolving Earth System Models (ESMs), in which the coupled nature of the components of Earth’s climate system are mathematically modeled, are all set as an Initial-Boundary Value Problem (IBVP).
It should be very clear from the previous post that the focus was exclusively on GCMs. It is very clear that the post addressed GCM models that are based on the interactions of the many various components of Earth’s climate system. Other, special purpose, models were not addressed.
Initial-Boundary Value Problem (IBVP)
A Partial Differential Equation (PDE) problem is said to be well posed if
1. a solution to the problem exists 2. the solution is unique, and 3. the solution depends continuously on the problem data.
The solutions to PDEs are arbitrary functions. General and mathematically rigorous proofs of the general existence, regularity, and uniqueness requirements for solutions of PDEs exist only for some simple cases. In particular they do not exist for the Navier-Stokes equations. Those well-posedness requirements, however, do not prevent applications of the concept of an IBVP to the present issues. To set a well-posed problem the correct number and kind of boundary conditions are also required. As a zeroth-order requirement, we always count the number of dependent variables and of their derivatives compared to the number of equations available to ensure that the numbers are the same.
We all know that a first order PDE in a spatial variable x and a time variable t has a unique solution (if it admits one) if and only if the solution u satisfies a boundary constraint (u=f on some boundary B of an open set U) AND/OR an initial value constraint (u=g for t=0). Absence of either of these leads to an infinite number of arbitrary solution functions. Boundary constraintand boundary value are generally interchangeable.
A boundary condition should be a function of x and t if the value of the unknown function also depends on x and t. For instance if a value is prescribed at some location B then u(B,t) = g(x,t)where g(x,t) is the forcing function imposed at B and can vary with x on B.
A special remark about transformations of boundary conditions is here necessary. If one spatially averaged the boundary condition g(x,t) one would obtain h(t) as boundary condition because the averaging destroys the x dependence. It follows that if the average is used, the boundary condition now becomes u(B,t) = h(t). This is clearly a completely different boundary condition than u(B,t) = g(x,t). It follows obviously that solutions of the same PDE with the first boundary conditions will not be the same as solutions with the second boundary conditions. In this case the solutions, if they exist, would be different from the solutions of the original PDE and therefore invalid.
This situation frequently arises in a great many (almost all) numerical calculations, whether or not explicit averaging operators have been applied to the basic continuous equations. Averaged equations are the rule, and not the exception, for all complex problems. Discrete approximations are a form of implicit averaging. If a grid is refined to higher resolution, the boundary conditions can change as described above. For example, the topology, as seen by the discrete equations, of the boundary surface itself can be effectively changed. The location of a solid embedded in a flow field will also change unless the grid refinement is carried out in a manner that considers this effect. These lower-order numerical artifacts prevent the order of the numerical method from reaching the theoretical asymptotic range, and can in fact result in the application order of the method to be less than unity.
In order to simplify an otherwise unsolvable equation, it arises often in practice of fluid dynamics that a change of variable involving averages is done: u(x,t) = U(x,T) + u'(x,t) where U(x,T)is the temporal average of u(x,t) over some interval [t,t+T] with T constant and u'(x,t) is a “fluctuation” around the average postulated to be with a temporal average 0. The result of this transformation is that the equation is no more naturally closed and empirical ad hoc closures are necessary.
Another far reaching consequence is that this transformation only simplifies the original equation if it is postulated that the short time scales of u'(x,t) do not interact with the larger time scales of U(x,T).
This is typically not the case in spatio-temporally chaotic systems where the time scales interact and U must be written as U(x,T,u'(x,t)) which defeats the original purpose which was to “decouple” the short and long time scales. Of course a similar change of variable could be done with a spatial average instead of the temporal average but the consequences would be identical.
ILL-Posed Initial-Boundary Value Problem
It has turned out that calculated GCM results indicate that the equation systems that form the basis of GCMs have resulted in ILL-Posed Initial-Boundary Value Problems. The numerical solutions do not depend continuously on the initial data, so Requirement 3 above is not met. Additionally it is not known if a unique solution exists so that Requirement 2 can only be postulated.
Analyses of the continuous equation systems, discrete approximations to these, and the applied numerical solution methods to establish a theoretical basis for the observed calculated results is far beyond the state-of-the-art for spatio-temporal chaos.
The hyperbolic formulation of the hydrostatic balance model for the momentum equation in the vertical direction, the basis of the dynamical cores for the atmosphere and ocean in several GCMs, has been shown to have complex characteristics; the equations are not hyperbolic under the conditions for which they should be. The ramifications of this result include; (1) artificial, purely numerical, growth of all wavelengths of perturbations, and (2) questions related to boundary-condition specifications. Item (1) is especially non-physical relative to the high frequency, very short wavelengths that in the physical domain are responsible for dissipation that stabilizes fluid flows.
When discussion are focused on mathematical matters, the universally accepted nomenclature should form the basis of word meanings. In this regard, GCMs using the hydrostatic approximation represent ILL-Posed Initial-Boundary Value Problems.
Chaos
The WG1AR5 Final Report includes Glossary III that defines the terms as used in the report. On chaos, the Glossary says:
“Chaotic A dynamical system such as the climate system, governed by nonlinear deterministic equations (see Nonlinearity), may exhibit erratic or chaotic behaviour in the sense that very small changes in the initial state of the system in time lead to large and apparently unpredictable changes in its temporal evolution. Such chaotic behaviour limits the predictability of the state of a nonlinear dynamical system at specific future times, although changes in its statistics may still be predictable given changes in the system parameters or boundary conditions.”
This definition applies to temporally chaotic systems where the dynamical parameters (pressure, temperature . . .) depend only on time and the dynamics are governed by a finite number of nonlinear ordinary differential equations (ODEs). A system such as the climate system is governed by nonlinear PDEs so that variations in space are as chaotic as variations in time. As the perturbations in spatio-temporal chaos propagate in space, which they cannot do in temporal chaos where space doesn’t exist, the dynamics of spatio-temporal chaos has little in common with the mere temporal chaos and is much more complex.
In particular the ergodic theorem which allows to connect temporal averages to the phase space averages is valid only for temporal chaos if it is ergodic (for example the famous Lorenz attractor) but has no equivalent for spatio-temporal chaos.
From there follows that there is no reason to expect a unique invariant probability distribution in spatio-temporal chaos which could be determined from boundary constraints alone. It is neither proven nor expected that spatial and temporal probability distributions are invariant and predictable on large time scales. A typical example of the variability of probability distributions on large time scales are the chaotic ice age and interglacial oscillations. These oscillations illustrate that it is not only impossible to predict their dynamics but it is also impossible to predict probabilities that this or that particular event takes place.
A current error for those not familiar with nonlinear dynamics is to exclusively assimilate the chaos in climate to the very short term fluid fluctuations like turbulence. While these short term fluctuations are indeed chaotic and lead to the unpredictability of the weather which is the base on which the climate is defined, the chaos in the climate is also due to nonlinear interactions at longer time scales and is not limited to fluids. Ice dynamics, clouds, biological phenomena and variations of astronomical parameters contribute to climatic spatio-temporal chaos yet they are neither represented by fluids nor by short time scales.
Here it has to be noted that boundary and initial conditions must be specified prior to solving any given PDEs. This is particularly difficult for the climate system. A boundary of a physical 3D system is necessarily a surface so giving a boundary condition means to prescribe the value of the unknown functions for every point and every time at this surface.
Yet these values are by definition unknown because they depend on the nature of the unknown function inside the boundary and therefore cannot be prescribed à priori. In the most favorable case when at least the spatial average of a parameter could be prescribed on the boundary it would still not allow to determine correctly the unknown functions because the spatial average operator destroys the spatial variability so that the boundary condition becomes u(x,t) = g(t) at the boundary B instead of the correct u(x,t) = g(x,t) at B. This has for consequence that the solutions computed with h(t) as boundary condition are invalid.
The phrase ‘boundary condition’ appears 47 times in the entire WG1AR5 report, is used in the Glossary but not defined there. The phrase ‘boundary value’ is used very infrequently, and also is not defined in the Glossary. The word ‘constraint’, and variations ‘constraints’ and ‘constrained’, are widely used in the WG1AR5 report. Constraint is not defined in the Glossary.
Boundary Value Problem (BVP)
There were extended discussions of this concept within the framework of GCMs at the previous Climate Etc. post, beginning at this comment. Several additional comments have been posted over there.
The BVP characterization offered by Professor Steve Easterbrook is widely cited. Professor Easterbrook said:
For understanding climate, we no longer need to worry about the initial values, we have to worry about the boundary values. These are the conditions that constraint the climate over the long term: the amount of energy received from the sun, the amount of energy radiated back into space from the earth, the amount of energy absorbed or emitted from oceans and land surfaces, and so on.
The first of these is indeed a boundary condition. The second is not a boundary condition, and additionally is incorrect both mathematically and physically. Specifying the energy, or mass, leaving a system violates the fundamental principles of energy and mass conservation. The energy absorbed or emitted by material interior to the system are calculated by the model equations; they are not specified.
Computational Fluid Dynamics and GCMs
In many discussions of models and numerical methods and GCMs, the relationship between Computational Fluid Dynamics (CFD) and GCMs comes up. These, of course, are related as fluid motions are at the heart of the dynamics of the atmosphere and oceans.
Generally, CFD applications are very significantly advanced in critically important aspects compared to GCMs. Very significant research and development efforts have been applied to CFD models, methods, software, and applications over several decades. Fully Verified and Validated commercial-grade CFD software, ready for a variety of everyday engineering applications, is a mature market outside the framework of research and development.
GCMs on the other hand are, relatively, more or less under constant research and development. Earth’s climate system is vastly more inherently complex than all and any CFD applications because the latter deal uniquely with Navier-Stokes equations while the former must include, among others, chemical, biological and astrophysical changes as well as many critical phase change processes leading to clouds and ice cover dynamics.
Frequently within these discussions the fact that CFD is applied to various aspects of commercial aircraft is noted. Of course that’s correct. However, these CFD applications are not related in any way whatsoever to the safety of commercial aircraft flight. Moreover the commercial CFD application are certified only for precisely specified ranges of the dynamical parameters. Typically the aircraft behaviour in stall conditions which is fundamental for the safety is outside of the specified range of parameters.
The safety and flight worthiness of commercial aircraft are completely determined by the independent Federal Aviation Administration (FAA). Flight tests determine the safety and flight worthiness of commercial aircraft. Safety and flight worthiness of commercial aircraft are not functions of any CFD calculations. After all, aircraft had been determined to be flight worthy for decades before CFD entered the picture.
It is an obvious fallacy to say, “You’re safe flying in commercial aircraft”, and then conclude, “Therefore GCMs are correct.” CFD and GCMs work with very different systems but, as already mentioned, CFD for aircraft dynamics is used for a specified range of fundamental parameters that have been Validated in wind tunnels, while GCM are supposed to work for all ranges of parameters and cannot be tested in wind tunnels.
For the most part, almost all applications of CFD to aircraft focus on a very limited sub-set of fluid dynamics, mainly turbulence, using a limited number of Validated parameters that can be directly related to the physical phenomena and processes of interest, and the states of the fluid that will be encountered in the physical domain. Numerical methods are a second focus and are deeply investigated. Relative to spatial resolution, numerical grids for CFD applications per unit of total modeled volume contain more cells by several orders of magnitude than GCM applications.
Qout = Qin
Discussions at CE and . . .aTTP more or less centered around the concept that at some undefined future time, when averaged over the entire planet for some, also, undefined time period, the out-going radiative energy at the Top of the Atmosphere (ToA) will be equal to the in-coming radiative energy. This hypothesis seems to be the basis for the argument that the “final state”, also frequently characterized as an “equilibrium” state, is determined solely by “the boundary conditions”.
Note that we already know that an “equilibrium” state is never going to happen. Given that chaotic response is observed in GCM calculations, steady state, and stationary state cannot be applied, so unsteady state must describe GCM results.
Also note that to postulate Qout = Qin, even in average over a time T, it is necessary to postulate that no energy sinks or sources (phase changes, chemical reactions, storage) existed in the system during the time T. Additionally if the surface where Qin and Qout are defined is such that only radiation fluxes exist and one is interested only in the non-reflected fraction of the incoming radiation, it is necessary to postulate that the reflectivity stayed constant during the time T.
Last but not least we must strongly remind what has been already said above. Postulating “Qin = Qout” through some surface has for a trivial consequence that the total energy in some volume is constant (see Gauss theorem). This tautologically true statement has nothing to do with boundary conditions because it is true for any arbitrary volume, any arbitrary boundary, and any arbitrary value of the dynamical parameters for which “Qin=Qout” is postulated true.
In particular, this tautology gives no information whatsoever about the dynamics of the system where any arbitrary energy and momentum distribution may exist as long as the total energy is conserved and we may be reasonably sure that it will be indeed conserved everywhere and for all times.
The equality condition is used with some GCMs as the target while tuning the model by use of variations in the many parameterizations that are critically important to the degree of fidelity of calculated results with the physical domain.
Earth’s climate system is open with respect to energy; energy both enters and leaves the system. It is yet another universally accepted concept that the energy (and mass) leaving a thermodynamic system cannot ever be specified. The energy leaving a system cannot be set as a boundary condition, boundary value, or boundary constraint. This statement is correct no matter how far away is future time, or for how long the average is taken. The energy, or mass, leaving a system cannot be specified because that act in itself violates conservation of energy, or mass, and other foundational concepts of mathematics.
The argument seems to claim that energy conservation is the the only part of the system that matters for the dynamics. Initial conditions don’t matter, turbulence doesn’t matter, chaos doesn’t matter, ill-posedness doesn’t matter, parameterizations, and tweaking them, don’t matter, tuning doesn’t matter, discretization doesn’t matter, numerical solution methods don’t matter, application grid resolution doesn’t matter, inherent weaknesses of the continuous equations, especially the parameterizations, don’t matter, the known limitations and uncertainties of many of all these aspects don’t matter, among others.
An easy thought experiment which has never been done in practice to our knowledge would be to run a GCM with initial conditions specified as “Gulf stream exists at t=0” and “Gulf stream doesn’t exist at t=0” while the boundary conditions are identical for both cases. It is beyond any reasonable doubt that the computed solutions and their statistics (averages, standard deviations, and higher order momenta) would be extremely different, This experiment would represent a numerical demonstration that initial conditions matter on all time and space scales and for all parameters .
In contrast, considering the possibilities associated with the long list of aspects that don’t matter, it seems possible that these aspects have resulted in models, methods, software, and application procedures for which the initial conditions and the boundary conditions don’t matter.
This is the very foundation of the present post. So far as we are aware, the “boundary conditions” that solely determine the “final state” have never been identified. Neither have the future time at which this state is attained and the time-period over which this state will persist. By what mechanisms an open system that is clearly operating far from equilibrium will attain such an equilibrium state has never been defined. The wide range of significant time scales in Earth’s climate system, with significant interactions between sub-systems operating at different time scales, and the chaotic trajectories associated with all changes and interactions, present a challenging modeling and calculational problem. The dynamics make a big difference in the overall energy balance and are chaotic.
In computational fluid dynamics terms the problem with the boundary condition argument is that it ignores the influence of the dynamics of the system on the distribution of energy within the system. Turbulence for example is a powerful mechanism for energy redistribution from inertial scales to ultimately heat. The distribution of energy in the system can have a quite significant influence on the energy leaving or entering the system. For example turbulent processes such as convection and clouds play a large role in terms of the top of atmosphere energy balance. Another example is Rossby waves which modulate the equator to pole temperature gradient and thus the distribution of energy radiated to space. And this distribution determines the total amount radiated to space.
Computational fluid dynamics is based in large part on the insight that understanding the dynamics and thus the distribution of energy is critical to understanding the system even in total energy balance terms.
Recently, several papers have appeared that document some of the effects of dynamics on total energy balance. Zhao et al [Ming Zhao et al., 2016: Uncertainty in Model Climate Sensitivity Traced to Representations of Cumulus Precipitation Microphysics. J Climate, 29, 543-560] dealt with the effect of microphysics of cloud sub grid models on the ECS of a GCM and found that the effect was significant. Similarly, when the French IPSL modelling group recently improved the clouds and convective parameterization of its main model, the ECS reduced (per AR5 Table 9.5) from 4.1 C to 2.6 C. While the changes are small in terms of total energy fluxes, they are quite significant when compared to the total flux perturbations induced by changes in greenhouse gases and thus are quite important to what we care about in the system.
The dynamics make a big difference in the overall energy balance and are chaotic. Thus feedbacks mediated by these dynamics are critical to determining the effect of the forcings. Quantifying the dynamics is critical to the, often, small perturbations we are really interested in. Thus, the “boundary value” problem explanation is simply wrong and likely to sow confusion.
Here’s the Question
Within the framework of GCMs and all other factors summarized above,
- (1) identify the boundaries of the physical domain that are represented in GCMs, e.g define the surface B which constitutes the invariant boundary of the whole system under study.
- (2) describe the Boundary Condition(s) (BCs) that are imposed on the boundary, and
- (3) describe the equation(s) and dependent variable(s) to which each BC that applies at the boundary B, e.g prescribe explicitely N functions Gi(x,t) defined on B such as for all dynamical parameters Fi(x,t) defined on B we have Fi(x,t) = Gi(x,t) for all x included in B.
Suggest a mechanism allowing to obtain a unique solution of the dynamical equations depending only on the boundary conditions and justify the time scale T at which this mechanism would start to operate.
References
G. Browning and H.-O. Kreiss, (1985). Numerical problems connected with weather prediction. In: Murman E.M., Abarbanel S.S. (eds) Progress and Supercomputing in Computational Fluid Dynamics. Progress in Scientific Computing, Vol 6, p. 377-394. Birkhäuser Boston
H.-O. Kreiss, (1980). Problems with different time scales for partial differential equations, Comm. Pure Appl. Math., Vol. 33, p. 399–439.
J. Oliger and A. Sundström, (1978). Theoretical and practical aspects of some initial-boundary value problems in fluid dynamics, SIAM J. Appl. Math., Vol. 35, p. 839–866.
R. Byron Bird, Warren E. Stewart, and Edwin N. Lightfoot, (1960). Transport Phenomena, John Wiley & Sons, inc. New York.
Marlow Anderson, (2009). Who Gave You the Epsilon? & Other Tales of Mathematical History, The Mathematical Association of America, Washington DC.


As a civil engineer who done a little non-linear modelling of hydraulic systems (a long time ago) the need for initial conditions seems obvious,and more importantly the unreliability of predictions due to inaccuracies or variations in initial conditions. However, as someone who does not follow developments in climate change modelling, am I to take from this that climate modelers are mostly using steady state models as opposed to dynamic models with specified initial conditions. I find this hard to believe. Am I interpreting the article incorrectly? If not, is there a counter argument posted anywhere defending the value of steady state models?
The models are dynamic models but its assumed the initial conditions don’t matter. As is commonly said in climate modelling:
Weather is an initial value problem
Climate is a boundary value problem.
Implicit in a boundary value formulation is the idea of steady state. So although the models are not steady state models…their results only make sense in steady state context.
Seems to me there is a fundamental underlying problem. Quite clearly, the mathematics simply do not support making distant predictions on the planets climate. The impact (if any) on man’s CO2 emissions is unknown. So why do folks claim they come up with a mathematical solution?
I think there is a fundamental lack of integrity on the part of many championing “climate change”. Rather than accept the obvious, the “ends-justifies-the-means” is the accepted theology. Clearly, a faction is hell-bent on imposing their will on everybody and will resort to any means (including violence) to prevail.
Application of this theorem to an equation for conservation of the total energy of the atmosphere led to requirements for that energy to be constant.
This would require the energy in the atmosphere during a major cold phase of a major ice age to be equal to the energy in the atmosphere during a major warm phase in between the cold phases.
This is clearly not correct.
It only needs a global balance. Think oceans.
So far as we are aware, the “boundary conditions” that solely determine the “final state” have never been identified.
Earth climate does not have a “final state”, there are “never ending cycles”.
Correct me if I’m wrong, but the boundary conditions are relatively straightforward – the energy coming in from the sun. Also, we do not want to predict a “final state”, we want to predict what conditions will be in 10, 20 50, 100 years time. This initial conditions are the state of the climate right now – we then model forward in time from that. If there is someone more expert out there, correct me if I’m wrong, I’m a bit rusty on this stuff. (This stuff must be frying the brains of those who just want to believe what they want to believe – on both sides of the debate. Many could do with a bit more humility.)
Even if the radiation coming in from the sun is straightforward (not sure it is), what the author is saying (I believe), is that the energy radiated out into the dark of space depends on the solution of the dynamic equations.
Even I would be surprised if the climate geniuses do not compute the outgoing radiation as a function of clouds, etc…, i.e. the dynamic state?
“This initial conditions are the state of the climate right now…”
From a prior discussion probably here that I cannot source, no. I believe they are spun up and in the ballpark as they driveby the start time. They reach an equilibrium or steady state. Yes, I could be wrong.
They reach an equilibrium or steady state
Never in the history in any real data proxy did earth temperature or sea level reach an equilibrium. There have always been cycles.
Pope’s
Agreed. Simply using the average temperature at any given time without knowing what you are recording or what transpired to affect that change is a road to nowhere.
Earth may give the illusion that is in equilibrium, it is not, never has been, never will be. The satellite era provides the only tangible opportunity to understand the mechanism’s.
Regards
procedures for which the initial conditions and the boundary conditions don’t matter
initial conditions don’t really matter for much. Earth temperature cycles in bounds, boundary conditions do matter. Oceans thaw and it snows too much when earth is warm. Oceans freeze and it snows too little when earth is cold. these are the boundary conditions that matter.
land drifted and ocean currents changes and more warm tropical water circulated in polar regions, supporting more sequestered ice on land with more ice flow and breaking off and thawing and cooling from more reflecting and cooling. These changing boundary conditions matter.
The argument seems to claim that energy conservation is the the only part of the system that matters for the dynamics
A cold earth, in a major ice age holds less energy. A hot earth in a major warm period between ice ages holds more energy. energy is not conserved in these states, A hot earth has more IR out for many years, the result is a bunch of sequestered ice that can cool with thawing and reflecting from an earth that holds less energy.
I know that it is highly presumptuous of me to comment on this post, I will stick my neck out as I did come away with some questions:
If climate is neither solely an initial value problem, nor solely a boundary constraint problem, then what kind of problem is climate?
Is the constraint on climate prediction our current physics? mathematics?
If, as seems from the above discussion GCMs are not fit for purpose, what is needed to be able to predict climate? Are there components of GCMs salvageable to build a new system?
Thank you for any consideration of the above. Regards
As far as I am aware it is a non-linear (chaotic) system which requires precise specification of both the initial conditions and the boundary conditions. In non-linear systems, small differences in specifying either of these can lead to large variations in predictions (meaning that they are unreliable). The non-linearity is an attribute of the physics of the systems. I get the impression from the article that current models are treating the systems as steady state which are less chaotic but not realistic. I find that hard to believe, so, again, someone should correct me if I’m interpreting this wrong. help! – This is important.
brian, current climate models are time accurate so they are not “steady state” models. However, chaotic processes like turbulence,clouds, and convection are treated by models that assume they can compute the “average” behavior of these processes. There are well known flaws enthuse models. No one knows how inaccurate these flaws make the climate model outputs.
RiH, I don’t know the answer to your question as to what is needed to be able to predict the climate. It’s an open question whether its “predictable” and what degree. It depends on unknown properties of the attractor. The question of computability is a separate question. it is computable only if the attractor is sufficiently attractive. We simply don’t know.
It’s simply not a problem to be solved.
A complicated one :) But one that doesn’t matter because “political solutions” are “known.”
What is known is the problem is less than half as bad as it was projected to be.
then what kind of problem is climate?
There is not any problem with climate, it is a series of well bounded repeating cycles that are self correcting.
The problems are all with the wild flawed theories and flawed analysis.
Great article. The language of mathematics is the only hope for climate studies.
It is even crazier than the article elucidates here. The simple fact is that planes fly safely because every new aircraft crashes many times, taking out test pilots before the final airplane is given certification. These crashes are studied, and the unexpected failures are fixed. Modelling, simulation (which uses simple lift/drag curves, not CFD), and experience only get things so far.
This, in general, is the difference between engineering and ‘science’. Engineering produces truths through experimentation and verification in the real world, whereas science produces textbooks that make the academics feel warm and fuzzy, but nothing more.
The simple fact is that planes fly safely because every new aircraft crashes many times, taking out test pilots before the final airplane is given certification.
I believe this is not likely true. I would like some documentation that: “every new aircraft crashes many times, taking out test pilots before the final airplane is given certification”.
Speaking from experience, certainly the two planes I worked on in my career follow the pattern:
https://en.wikipedia.org/wiki/Accidents_and_incidents_involving_the_V-22_Osprey
https://www.verticalmag.com/news/aw609-crash-final-report-points-oscillations-flight-control-laws/
In particular, one of the many V22 crashes involved ‘settling with power’, a phenomenon involving stalling in ones own rotor wash; something not simulated with either CFD or simulation models.
This is why we tend to fly in aircraft that were designed half a century ago. Most new aircraft are merely slight tweaks of older designs. When a truly new design emerges (such as the tilt-rotor), you can be some test pilots are going to eat it.
http://www.bbc.com/future/story/20140414-crashes-that-changed-plane-design
In particular, one of the many V22 crashes involved ‘settling with power’, a phenomenon involving stalling in ones own rotor wash; something not simulated with either CFD or simulation models.
Sounds like an operations error, not a design flaw. If you sit on top of downwash that must come back up, you fall. That could be modeled with proper understanding of what really does happen.
The V22 has a very small diameter rotor with high velocity. Such a configuration is prone to this problem, so it was not entirely unknown. What was unknown was the exact parameters of the danger, which an unlikely pilot discovered.
Great point, nickels.
The IPCC and others use ensembles of climate models because it is well known that none of them are “correct.” And so a range of outputs are then used to “represent” the “range of possible outcomes” in the “predicted” future climate (atmospheric CO2, temperature) trajectory. What wrong with this statement. Ans. “just about everything.” They also know that because of the size and scope of the global climate system there is zero hope that it can actually be modeled in the strict or correct sense of the term. I love this post by Dan Hughes and Tomas Milanovic because it defines the nature and bounds on what can and cannot be done in climate modeling, and therefore on what conclusions can be drawn from the climate modeling. If you do not have background in fluid dynamics, thermodynamics, statistics and modeling you can not possibly understand and appreciate the challenges involved. The consensus will say “it doesn’t matter,” and maybe (or not, that they know this) and they are simply trying to present a representation of the future climate system to present a best possible representation or “paint the picture” or how the climate system could evolve over time to serve in policy discussions and decisions. Again, what’s wrong with this statement; and again Ans. “just about everything.” If you know that there are missing variables in your modeling (some of which you know are missing, others you may not even know about), but you represent it as a result that is used to justify policy making, knowing that the model is incomplete.. yes … there is in fact is a huge amount wrong with this picture. I did not use the words “game” or “gaming,” somewhat of a problem with intellectual honesty.
A typical example of the variability of probability distributions on large time scales are the chaotic ice age and interglacial oscillations. These oscillations illustrate that it is not only impossible to predict their dynamics but it is also impossible to predict probabilities that this or that particular event takes place.
The ice core data explains ice ages and they are not chaotic. A sufficient supply of warm ocean water in cold places will lead to a major ice age because there is an ample supply of water and energy to produce an ample supply of ice. That condition was present ahead of every major ice age and a major ice age followed that condition. The ice spread out and cooled with reflection and thawing until the supply of sequestered ice was depleted and every major ice age ended as the depleted ice retreated.
The last major ice age was not followed by a major warm period because, finally, enough ice was sequestered in cold places and there was not enough meltwater left to raise the ocean to the previous higher, warmer levels.
Now, lesser warm periods are followed by lesser cold periods and the lesser cold periods are followed by lesser warm periods. Nothing chaotic here.
Chaotic is simply something you do not understand and not chaotic is simly something you do understand. Climate is self correcting, not chaotic. Some chaotic seeming events still do not drive climate out of bounds. As the balance between ice sequestered on land and water in the oceans, cycled back and fourth, there was never chaos. Ice cores were saved for us to study and understand.
@pope – When I use the term chaotic I’m not referring to random or simply unpredictable change, I’m using it the way Chaos Theory people use it to mean non-linear systems. Perhaps it is best to avoid using chaotic as a term for this as it has other meanings to people.
I’m using it the way Chaos Theory people use it to mean non-linear systems
Non-linear does not mean the same thing as Chaotic.
Ditto to PCT. Non-linear very much does not imply chaotic.
~w, whose graduate work involved non-linear but non-chaotic systems.
It might be worth considering constraints implicit in the assumption that a function T(r) exists. In classical thermodynamics, temperature enters as an integrating function rendering a partial differential equation exact so that integrals between states become path-independent. Properties are then independent of thermal history. Obviously, hysteretic systems lie beyond the pale. For thermodynamic equilibrium, T is constant. For steady states one may assume a function T(r) exists independent of the manner in which surface potentials are applied. The thermodynamic temperature is not a physical parameter expressible in the p’s and q’s of a mechanical system. In fact, it is not a difficult exercise to show that boundary temperatures suffice to define internal thermal profiles as those minimizing steady-state dissipation, the work required to maintain even non-linear steady states.
Gotta love this article. In climate “science” liberties are taken in defining such things as equilibrium, so that we can calculate an equilibrium climate constant (ECS) using equilibrium equations. When the results from the GCMs differ from the measured results, then the models must be correct and the measured results wrong. I have yet to have anyone come close to explaining how this is correct, but I am willing to listen.
at&b, the way nick stokes explains it, if we assume the models are correct, then what happens in real time is like a single trial run of the models. Reality could run hotter or cooler than the unerring model (in the same way that trial runs of the models themselves do)…
So we start with the models are correct. This is known to not be the case. Models are not correct as they do not and can not take everything into account (clouds for instance), but sometimes over simplifications are useful. However, to state that the values predicted by the models are superior to the real time values is still perplexing to me.
So we start with the models are correct.
No, that’s missing the point. The point is that even if the models were perfectly correct, the real world would still just be like one random run across an ensemble of possibilities.
So — make sure when comparing the real world to the models that you properly handle the associated probabilities and statistics.
“So — make sure when comparing the real world to the models that you properly handle the associated probabilities and statistics.”
This is the point. The models put the ECS at 1.5 to 5. The real world puts ECS at 1.5 to 1.7. If you look at temperatures the models are running hot beyond the statistical significance when compared to the measured temperatures. The real world data does not support the models.
The article discounts the value of the energy balance too easily There is an energy balance equation, but it is not Qin=Qout, it is Qin-Qout=Imbalance. Over periods of 30 years or so, an imbalance of only 1 W/m2 is easily measurable as a gain in heat content even though Qin and Qout are individually hundreds of times larger. The fact that there is an imbalance means that there is also an equilibrium state where the imbalance is zero. The current imbalance is measurably positive meaning we are below the equilibrium and Qin > Qout. The reason Qout is not keeping up with Qin is because adding CO2 suppresses the earth’s ability to radiate longwave, and its continuing growth means this imbalance exists because of the lag in response.
Energy Balance Models (EBMs) use a variant of this equation where the forcing change = response + imbalance
If you change the long-term forcing whether by solar variations, volcanoes or GHGs, you get an imbalance and a response. Eventually after the forcing stops changing, the response (usually defined in terms of the mean surface temperature) catches up and the imbalance goes away. That is the new equilibrium. Currently the imbalance is significantly non-zero, so we are in a transient state where the response is lagging the forcing change.
The article dismisses the concept of equilibrium that is the basis of EBMs such as that of Lewis and Curry (what would they say about this?).
Whether you want to call a forcing change a boundary value problem is semantics. The reality is that the climate is specified by the forcing, and climate change is dominated by the forcing change. EBMs take these variations to be linear and directly proportional when they are small, such as 1% from doubling CO2, but tipping points are another story.
… garbage in, garbage out. The climate models are unfit for the application trotted out by the climate-change religion. Period.
EBMs are based on observations, not GCMs.
As I said, garbage in, garbage out. Stop trying to hand wave through exceptionally complicated physics and accept the fact we are not in a position to predict the distant future. Pragmatically deal with the present.
OK, tell that to Lewis and Curry, then. They know when the climate is out of balance.
Like I said, garbage in/garbage out. If the mathematics are fundamentally flawed (and they are), the results are meaningless.
It’s energy conservation. This is not models. It’s observations and an energy budget. I have said nothing about models. Repeating your mantra shows only that you don’t understand what I said at all.
So you think you can predict the trajectory of the planet’s climate by simple qualitative hand-waving devoid of mathematical models? Wow.
Old mechanical engineering adage: There is no problem that ignorance cannot overcome.
Energy conservation is a guiding principle. If you’re not considering the long-term energy budget, you’re doing something wrong. If Qin > Qout, that heat is going into the heat content. If you suppress Qout, that increases the heat content.
“steady state is used to derive the Michaelis-Menten equation”
Yes. When chemists speak of equilibrium, they mean dynamic equilibrium, where there is a forward and back reaction occurring at equal rates. The situation where there is no reaction of any kind is of no interest.
Nick Stokes: The situation where there is no reaction of any kind is of no interest.
I gave the example of thermodynamic equilibrium being used in the derivation of the Clausius-Clapeyron equation, which in turn is used in climate modeling. Are you telling us that I am wrong?
As to steady state and dynamic equilibrium, the Earth is never in those states either. Is it?
“As to steady state and dynamic equilibrium, the Earth is never in those states either. Is it?”
Everything we know in science is subject to some sort of idealization. When you use Newtontian mechanics for something, there is generally a caveat about ignoring friction, air resistance etc. The point is that you can calculate the ideal state solution, then worry about how far you might be from ideality. So no, the Earth will never be in those states. Nothing ever is. That doesn’t mean we should abandon science.
There is an interesting issue with notions of equilibrium, though, which is properly considered as balance. Some process has to keep the balance (unless the equilibrium is truly not stable). That will be a time-varying process, and the use of equilibrium concept becomes appropriate when the restoring process is fast.
Consider airflow around a sphere. The oncoming flow smoothing diverts to pass by and then close in behind. What makes it do that? A pressure field, high in front of the sphere, and low behind. How did that field get there, and what keeps it there? Pressure (sound) waves. That is related to the divergence mentioned here.
A ball falling will set up and maintain this pressure field, even as it accelerated, and you can calculate the resulting flow assuming the pressure is sorted out on a rapid time scale. That is the incompressible approximation. But as the ball gets faster, the sound waves can’t do the job fast enough. Then you get to the radically different transonic and supersonic flow regimes. That is when the deviations from the notion of a near steady (“equilibrium”) pressure field matter. It is all a matter of timescale and degree.
Nick Stokes: Everything we know in science is subject to some sort of idealization.
Sure. Having used the thermodynamic equilibrium assumption that you disparaged to derive the C-C equation, the next question is: Has the C-C eqn been shown to be accurate enough in enough conditions for subsequent derivations to be provide insight or be reliable. But your initial disparagement of thermodynamic equilibrium was absolute, and that drew my criticism.
And the same can be said for the M-M equation, which has been shown to be accurate enough in a lot of settings, generally for first-order equations where the substrate concentration is large compared to the enzyme concentration. But not always.
Note also my comment to the authors about “inaccurate” versus “invalid”.
Yes Nick and Matthew except that as soon as you get to interesting conditions, there is massive separation behind the sphere and chaos comes into play. And that’s really where all fluid dynamics is really pretty weak. Similarly with convection. We have a pretty good handle on boundary layer turbulence but even large scale vortex flows are problematic (like Rossby waves).
The climate system is vastly more complex than aeronautical CFD that we are used to because of the role of energy transfer mechanisms which are often chaotic.
“thermodynamic equilibrium assumption that you disparaged”
I don’t disparage the assumption at all. I disparage the contention that we don’t know anything because the assumption is never fully met.
Nick Stokes: “Lack of gradients, implying lack of flows.”
It may be a rigorous definition, but in an earth context, it is absolutely useless.
that reads to me like disparagement.
Nick, I don’t think anyone is saying that “we don’t know anything.” The point here is that comparing the climate problem to a boundary value problem is misleading and is not technically true.
“that reads to me like disparagement”
Of that definition. But the Clausius Clapeyron equation is fine and useful, even on our earth on which not all gradients are zero.
I have the feeling you have swapped sides on this? Do you think there is something wrong with Clausius Clapeyron and its derivation?
David,
“comparing the climate problem to a boundary value problem is misleading”
I don’t think Steve Easterbrook’s article is misleading; I think it makes very well a point that I have often tried to make. The fact that the flow does not preserve what is known about the initial arrangement (because of mixing, which some like to call chaos) has the same consequence in both GCMs and CFD (and real fluid flow). Although the mechanics of solution require you to start with an initial state, all that really matters is that it isn’t badly unphysical. And to guard against the possibility that it is somewhat unphysical, you give it time to settle down before using it for results. What determines what you want to know is not initial state, but what happens to it along the way.
Easterbrook characterises that as a boundary value problem. It isn’t literally correct, because a lot of perturbations, like GHG growth, are (or were) implemented as a change in ppm of well-mixed constituents. And radiative changes aren’t exactly boundary. But Steve doesn’t make a point about literal bvp solution, and certainly not in what is quoted here. So I can’t see any point in haggling that.
And as I also try to emphasise, the lack of dependence on initial state is a blessing, because it isn’t known anyway. And it reflects the same in real flows. No-one tries to work out the initial state of a wind tunnel. It doesn’t matter.
Nick Stokes: I have the feeling you have swapped sides on this? Do you think there is something wrong with Clausius Clapeyron and its derivation?
In the beginning, you wrote that the definition of equilibrium used by Hughes and Milanovic was useless. I pointed out that equilibrium by that definition was used in the derivation of the Clausius-Clapeyron equation. If in fact the C-C equation is useful, then your assertion that the equilibrium assumption used in its derivation is useless is a false assertion.
Hughes and Milanovic wrote that results derived from the simplifications of the assumptions they provided would be “invalid”. I suggested that “inaccurate” would be a better adjective, and it would be worthwhile to investigate how inaccurate various simplifications are.
Applied to C-C and M-M eqns, and many others (if not all) expressions derived from idealizations, the question carries over: are they demonstrably accurate enough for the purposes for which they are used? For M-M they frequently are if there is thorough mixing of substrate and enzyme molecules and if the concentration of substrate is high; for active transport of substrate molecules to strongly localized enzyme molecules (hepatocyte endoplasmic reticulum), probably not so much. For C-C, the demonstration of sufficient accuracy in diverse conditions (e.g. before, during, after tropical storms and hurricanes, clear winter nights and cloudy summer days), not so much, if any; anything derived from them is questionable, almost for sure not accurate enough to use in modeling effects of changes in CO2 concentration..
Clausius-Clapeyron defines the vapor pressure at the vapor/water interface, and also exists because there is an equal flow from water to vapor as vapor to water at that interface. Chemical equilibria like Henry’s Law are also of this type. CO2 flows into and out of the ocean, but there is an equilibrium when there is no net change. It needs both a flow and an interface for its definition. It is a condition of no net flow, not a condition of no flow at all. Likewise Qin=Qout is a condition of no net energy flow. Equilibrium is a balance between two opposing flows in these cases.
Well Nick, recent results show that initial conditions do make a difference because of multiple solutions, sometimes close together for even RANS. Initial conditions determine which of these (perhaps many) solutions you find.
Easterbrook should have made his point without talking about boundary conditions. In any case, his point is largely untrue as recent results show. In any case, in the climate system, initial conditions often make a big difference for example the presence of ice sheets.
It is of course also true that initial conditions make a difference in wind tunnels too. There are hysteresis loops. If you start from an attached condition and increase angle of attack, you will eventually separate. If you now decrease alpha, the flow will remain separated in some cases for a large decrease in alpha. I have some flow viz in a tunnel from a Swedish flight controls person that is quite impressive in this regard. The range of alpha where there are at least two solutions is perhaps 10 – 15 degrees.
A lot of this thinking you are expressing here is due to biases in the literature. These multiple solutions are simply not reported.
For time accurate simulations, the issue is just beginning to be explored.
If you look at any of the many EBM studies (Lewis and Curry being one), the temperature change is only a function of the forcing change, not any details of the initial state. This would be more like a boundary value problem by definition.
JimD: The fact that there is an imbalance means that there is also an equilibrium state where the imbalance is zero.
Unlike the authors, you use the word “equilibrium” without discipline.
Equilibrium means no imbalance. Transient means there is an imbalance. For climate we would use long-term averages of the heat content trend to check the size and sign of the imbalance. How much better defined can it be? How do the authors define it? It seems very fuzzy. Any time the forcing is changing, which is almost always, even if defined over 30-year climate intervals, there is not an equilibrium and there is an imbalance. So in general Qout is not equal to Qin, and they are wrong to assert that. The imbalance is an important term that is at the center of climate sensitivity, especially EBMs.
The imbalance is an important term that is at the center of climate sensitivity,
Wow, climate sensitivity and imbalance both can be tossed out because there is no data that does support either of them.
JimD: How do the authors define it?
Lack of gradients, implying lack of flows.
In the climate context, it is when energy in = energy out. If Qin > Qout you get a gain over time due to the imbalance. This is a storage term or gain in heat content of the system. Equilibrium is when the heat content is not changing over time. A positive imbalance is when it is warming, which is the current transient state. This is all to do with energy flows and storage. Do they dispute that? They don’t mention imbalance or changing heat contents at all, which seems to be missing the big picture about what the balance equation really is, and why changing one of the terms in the balance matters so much.
JimD: In the climate context, it is when energy in
You asked how the authors defined it. Your usage is sloppy.
Energyout=Energyin over what time period?
I would choose a long period like 30 years. It is for climate after all. Their definition doesn’t mean much. Gradient in what? No flows of what? Energy flows are pervasive and critical to the understanding of the system which is defined by flows and storage rates. What does no flows even mean?
“Lack of gradients, implying lack of flows.”
It may be a rigorous definition, but in an earth context, it is absolutely useless. Heat from the sun flows in, and flows out again down a temperature gradient. You can’t have that equilibrium above 0K.
Steady gradients would be the only sensible notion of equilibrium. That is the E in ECS.
Nick Stokes: Steady gradients would be the only sensible notion of equilibrium.
That’s steady state.
Is “equilibrium” ever defined? Or used in other than the usual thermodynamic sense? As used in Pierre-Humbert’s presentation of the Clausius-Clapeyron relation (in Principles of Planetary Climate), it is the standard thermodynamic sense used by the authors here.
“Would be”: in all of the frequently cited climate literature, is it in fact ever defined that way and then used according to that definition? Even by your definition, there is no reason to think that the climate ever has been or ever will be in equilibrium, and plenty of evidence that it isn’t.
Nick,
Steady gradients would be the only sensible notion of equilibrium. That is the E in ECS.
At what time were those gradients last steady and at what future time will they again be steady?
MRM: That’s steady state.
This matter of steady-state (as I use it) and equilibrium (as used in Thermodynamics and by Hughes and Milanovic) is not as straight-forward or universal as I had thought. Nayfeh and Balachandran (p 1 in Applied Nonlinear Dynamics) say that “steady-state” is the limit as t -> infty. Of course, you might not have any evidence or proof that the limit exists.
Arthur Schultz, in Enzyme Kinetics, eqn 1.14, p 9, defines steady-state as I did, in which the time derivative of the concentration in each compartment is 0 (implying amount in – amount out = 0, at every t in an interval) and use it to derive the famous Michaelis-Menten equation. S. Wiggins, Introduction to Applied Nonlinear Dynamical Systems and Chaos, p 6, says that other terms for “equilibrium solution” include “fixed point” (really?), “stationary point,” “rest point”, “singularity”, “critical point”, or “steady state”. And so with other references. “My” usage appeared in some, but not all of the references that I checked. I should note as well that “steady state” is seldom in the indexes.
I recall this came up some months ago, and I started reviewing some of my references then.
It would seem that if someone were to try to make substantive claims based on derivations from an assumption, then they ought to define the term exactly and then stick to it. That is what Hughes and Milanovic did here. In Principles of Planetary Climate, Rymond Pierrehumbert used the definition of “thermodynamic equilibrium” as given here by Hughes and Milanovic to derive the Clausius-Clapeyron equation: in any system for which the thermodynamic equilibrium was not met exactly, the result ought not to be taken as accurate.
Nick Stokes, Jim D, and anyone else might have their preferences of how “equilibrium” ought to be defined, but for any consequences they wish to derive they ought to use the definitions rigorously; and they ought to accept that consequences derived from the standard definition do not apply when other definitions are used.
Yes Matt, the usage of “steady state” is quite confused in many common usages. The mathematical definition is I believe that all your time derivatives go to zero and the residuals of the right hand sides are all zero. Of course, these steady states can be stable, unstable, or saddle points. In the real world, there is never a steady state for lots of reasons.
Steady state is a mathematical construct to help us think about Reynolds averaged forms of the Navier-Stokes equations or structural dynamics. In the latter the theory of linear elasticity is really very nice and well behaved mathematically. Many laymen (and even CFDers) have a mental model based on linear structural analysis that they try to apply (often unconsciously) to turbulent CFD. Many bad decisions have resulted from this confusion.
dpy6629: In the real world, there is never a steady state for lots of reasons.
I first came across “steady state” in pharmacokinetcs: noe that the reference by schultz has the meaning that I learned, and that meaning is in all pharmacokinetics textbooks. In drug dosing, a true steady state may be achieved with prolonged IV dosing at a constant rate: after a sufficient time has passed, the concentrations of the drug in all the compartments will remain constant until the IV dosing rate is changed. So what I thought was a “true” definition might only apply in a tiny corner of the world. The usage may be common in chemical engineering.
“Quasi steady state” is a generally accepted term for this kind of system which is dynamic but averaged over time is constant. “Equilibrium” is often used as a shorthand.
Here’s the AMS glossary version
http://glossary.ametsoc.org/wiki/Quasi_steady_state
I’m not sure what the AMS reference is getting at but I’ve never heard of this idea except as an inadequate way to get a result when your code refuses to converge. When I looked into the NCAR model I found that they use eddy viscosity to model the turbulence in the boundary layer. Reynolds averaging is the standard method to treat turbulence and is a lot more justified than just claiming that turbulence is constant. Turbulence grows as you go downstream and evolves as the boundary layer changes so on time scales of days you must evolve your turbulence too as wind changes. Different air masses have dramatically different levels of background turbulence.
Again, you can define equilibrium as Tomas and Dan do, but it is a pointless definition, as it is inconsistent with the presence of a sun.
Steady state has a useful definition, which is that
1. Nothing changes on the time scale that you want
2. (a consequence) time derivatives can be omitted from equations.
Quasi-steady is a bit different. It says that you can ignore time derivatives in equations, but things can still change on the time-scale of interest. This might happen in forced movement of a very viscous fluid, say, and the momentum equation. The force associated with acceleration is negligible relative to the viscous stress and pressure gradient or body force, so you solve the equation without it. But the fluid moves.
I don’t see any point in haggling about the difference between equilibrium and steady state.
If you look into it further, though, there is always a time mechanism underlying steady state, which is the mechanism for dealing with deviations from it. For linear elasticity, that is the elastic waves.
“At what time were those gradients last steady and at what future time will they again be steady?”
A pointless question in the context of definitions. Terms like steady or equilibrium refer to the situation where the terms associated with time rate of change are negligible. Even if that doesn’t happen in practice, the definition is still meaningful.
It’s nothing to do with code. It’s a physical description.
Equilibrium = no flows
Steady state = constant flows
Quasi steady state = flows averaged over time constant
No code involved.
Nick Stokes. Again, you can define equilibrium as Tomas and Dan do, but it is a pointless definition, as it is inconsistent with the presence of a sun.
Geeezz Nick, you know Tomas and I did not define equilibrium, and we most certainly did not apply such a description to possible states of Earth’s climate system. Thermodynamics does not consider it pointless to define equilibrium.
Equilibrium = no flows
A state of no flows has never existed, and will never exist, in Earth’s climate system.
Dan
“Equilibrium = no flows
A state of no flows has never existed, and will never exist, in Earth’s climate system.”
So why do you go on about it? Talk about something useful.
Nick Stokes: I don’t see any point in haggling about the difference between equilibrium and steady state.
It depends on exactly what assumption has been made to derive a result. As I mentioned, steady state is used to derive the Michaelis-Menten equation, and steady-state can occur in the distribution of a drug during continuous infusion. I do not know if equilibrium ever occurs, but it has been assumed in derivations since as long ago as Boltzmann, and was used in deriving the Clausius-Clapeyron equation.
You could if you wanted define a climate (near) equilbrium of n years duration as a period of n years during which the global mean temperature (or something else of focus) had a time derivative of (nearly 0). Recently had such a period, called a pause, but hardly anyone called it an equilibrium (some writers asserted that, contrary to either equilibrium or steady state, energy was accumulating in the deep ocean).
Exploring the consequences of finely differentiated definitions and assumptions is really common in graduate school courses in mathematical disciplines like applied mathematics, statistics and physics. If you believe, or entertain believing, a result that was derived from an assumption of equilibrium (Clausius-Clapeyron?)), you might want to examine the exact definition and other assumptions made. Anything derived from the assumption of thermodynamic equilibrium is probably not believable about Earth Climate.
Back to the pharmacokinetic example, (near) equilibrium only exists when the drug concentration has gone to (nearly) 0.
I would suggest that everyone calm down and try to think analytically. One of Dan’s points I think is that there is a lot of loose use of terminology by those trying to explain climate science. I would agree that its not very helpful to do that as it just confuses the issues. It would seem Nick that you agree with this.
The main point here for me is that neither initial value problem or boundary value problem is really applicable in the context of Navier-Stokes equations. It’s much more complicated.
VTG, ECS of course is an idealized concept as the climate system will never really equilibrate with “fixed” forcings. That doesn’t in any way contract the thermodynamic definition of equilibrium but perhaps shows that ECS is not particularly well named.
Perhaps confused thinking is very common among scientists or those with scientific pretensions, but that’s not evidence of anything really.
In the climate sense, equilibrium is a state of no imbalance, i.e. one of balance, where Qin=Qout. Usually we are not in exact equilibrium but we can estimate the imbalance over a given set of decades. A positive imbalance means we are below the equilibrium temperature, and that is where we are now. More warming in the pipeline and ECS > TCR.
It is an equilibrium even if flows are involved. The question “What is the equilibrium temperature of a spinning object with an albedo of 0.3 and emissivity near 1 at Earth’s distance from the sun?” has the answer 255 K. It is perfectly valid to say this is an equilibrium temperature in those conditions, as it is to say how it would increase if the sun became 1% stronger. Objects have equilibrium temperatures under various fixed conditions.
There is an energy balance equation, but it is not Qin=Qout, it is Qin-Qout=Imbalance.
Temperature change, day and night, cloudy and sunny, summer and winter, shows that temperature is never out of balance. When temperature changes over time it means the factors that determine temperature did change, there is no proof that there is ever an imbalance. Actually, the basic laws of physics says each little mass is always in balance at that instant. It may be changing, because the things that influence it are changing, but it is always in balance.
Imbalance is a myth that is not supported by actual data. If you could measure imbalance it would be identified and be a part of the actual balance. Imbalance is a product of not understanding natural basic physics.
That’s the part you need to take up with Lewis and Curry. Their whole study falls apart if they can’t even use the measured estimates of the imbalance.
Their whole study falls apart if they can’t even use the measured estimates of the imbalance.
Estimates of anything are estimates, not measurements. Estimates of imbalance are not measurements.
Estimates are based on measurements of the rate of change of the ocean heat content. The ocean heat content is a real thing that has a value and units, not a “myth” at all. You use the term “myth” for something you don’t understand, and perhaps you don’t.
JimD, Energy balance methods are perfectly valid. The problem here is that you need to know the outgoing energy to use them and that outgoing energy is a result of the chaotic dynamics of the system. Energy balance methods also require forcing estimates that must come from measurements or other methods.
I don’t think the post “dismisses” energy balance methods per se. It just says that energy balance doesn’t tell us what the state of the system will be without a lot of other information.
If you have an imbalance of even 1 W/m2 over a period of 30 years, it produces a measurable change in heat content. This is similar to what adding CO2 is doing by shifting the forcing. Similarly small changes in the sun during the 11-year cycle, or volcanic activity also show up in the temperature. By not recognizing how even a little forcing produces measurable changes in the system, they are losing sight of the importance of changing the forcing by many W/m2 on the heat content.
” The problem here is that you need to know the outgoing energy to use them”
I think the main problem with EBMs, or any methods based on the history, is that it attempts to measure a change ratio when there hasn’t been very much change, so there is a lot of inaccuracy in the ratio. GCMs of course can set up a much greater change (eg doubling). GCMs can also push a lot further toward steady state following change.
Nick Stokes: I think the main problem with EBMs, or any methods based on the history, is that it attempts to measure a change ratio when there hasn’t been very much change, so there is a lot of inaccuracy in the ratio.
That is a good point, but it does concede the problem that TOA imbalances are poorly measured, and it is only 1 reason why.
That reminds me of a question I have asked before. Has the amount of energy that is stored via photosynthesis been estimated? Is an extremely low upper bound supported by evidence?
“Has the amount of energy that is stored via photosynthesis been estimated?”
Yes. From a carbon cycle representation, eg
NASA, 121 Gtons/year of carbon are reduced in photosynthesis. From Wiki
“Today, the average rate of energy capture by photosynthesis globally is approximately 130 terawatts”
That is about 0.26W/m2, pretty small. But the main thing is, the energy is given back when the reduced carbon is re-oxidised, which is soon enough, whether by respiration (half is immediately used by plants for respiration), decay, burning etc.
Nick Stokes,
Do you know where to find figures on how much C is tied up in the biosphere now, and how much was tied up when the planet was warmer than now, e.g. during the Cretaceous, and Paleogene Periods (Paleocene, Eocene, Oligocene Epochs)?
The NASA diagram that I linked says there were 610 Gtons C in vegetation. I expect it would be very hard to estimate for long ago.
Nick,
Thank you. IPCC AR4 WG1 Ch 6 says 3000 Gt C tied up in the biosphere now and about 300 to 1000 Gt at the LGM – that is a factor 3 to 10 increase since the LGM. Fossil evidence suggest it was substantially higher during warmer times. But I haven’t managed to find an authoritative estimate of the Gt C.
[Biosphere includes biomass in soil and oceans]
No, it doesn’t, as repeatedly pointed out before. It says 3,000 now and 300-1000 less than that at LGM ie 2300-3000 at LGM.
Should read 2000-2700 at LGM
Nick Stokes: That is about 0.26W/m2, pretty small.
Thank you.
Correct. My mistake:
https://www.ipcc.ch/publications_and_data/ar4/wg1/en/ch6s6-4-1-4.html
“The reason Qout is not keeping up with Qin is because adding CO2 suppresses the earth’s ability to radiate longwave”
Not really. According to CERES LW radiation to space is flat or increasing. It is increased absorption of SW that keeps Qin ahead.
https://geosciencebigpicture.files.wordpress.com/2018/04/ceres-toa-all-sky-inverted1.png
The surface warming response drives up Qout to compensate for the effect of the CO2 which would be -0.5 W/m2 over this period without the warming. This is how warming works. The albedo change is part of the positive feedback that enhances the response.
Which albedo change? Less snow and ice? Fewer clouds? More barren land? Data on all these is equivocal.
Where do you get the negative .5 watts “without the warming”? Last I heard you were all about the 2-3 watts reduced LW to space “in the wings” of the CO2 spectrum claimed by MODTRAN.
For albedo, all of the above contribute, and clearly it has changed in a net positive feedback sense. In a period of 18 years the CO2 forcing changed by 0.5 W/m2. Without warming, the LW part would have decreased by that much. The total CO2 change up to 2018 from pre-industrial is about 2 W/m2, but much is already compensated by warming.
Radiative effects are not compensated by temperature. They can be saturated to extinction such that no further Qout reduction takes place with increasing concentration, but electrons bumped to higher rotational/vibrational levels do not quit. They keep banging away.
A warmer earth radiates more longwave. This is how the earth compensates for the reduction from CO2.
“In 18 years the CO2 forcing changed by 0.5 W/m2.”Is this a measured or a modeled value? Regarding albedo, do you mean a daytime albedo, a nighttime albedo, or some sort of an average?
It’s calculated from the standard formula for a change from 369 ppm to 406 ppm.
Decreasing albedo is the only thing that can increase the net solar radiation short of the sun itself strengthening, and no one suggests the latter has happened in this period of 2000-2018.
It’s not albedo, at least not clouds. Clear sky shows the same trends, and MODTRAN remains out to lunch.
https://geosciencebigpicture.files.wordpress.com/2018/04/ceres-vs-modtran.png
It the radiative transfer program is out to lunch, what is the standard formula for 369 to 406?
Reduction of snow cover and sea ice are important albedo factors, probably larger than cloud changes. There may also be some increased solar absorption due to more water vapor, but that would be small.
The formula is 5.3 ln (CO2new/CO2old) W/m2. This comes from the standard 3.7 W/m2 per doubling.
It cannot increase long term accuracy of GCMs to continue ignoring changes in solar activity.
Ignoring changes in solar activity are some of the smallest things about GCMs that are wrong, they ignore the self correcting factors in climate.
It snows more when oceans are warm and thawed and ice increases. It snows less when oceans are cold and frozen and ice depletes. GCMs don’t even consider ice as anything other than a result. They don’t consider ice is a part of the self correcting response that limits the bounds of climate change.
Stands to reason that the Medieval, Roman and Minoan warming periods were not caused by the sins of modernity, any more than warming during the last half of the 20th century had anything to do the Greek god Helios nd his Sun Chariot.
“It cannot increase long term accuracy of GCMs to continue ignoring changes in solar activity.”
People seem to be happy to say just about anything about GCMs, without checking on the facts. Of course GCMs account for change in solar activity. It is very easy to do, as solar flux is specified at each time step.
Here is the GISS discussion of how they do it in model E. Here is the plot of what they input for the CMIP 5 simulation:
https://data.giss.nasa.gov/modelforce/solar.irradiance/tsi_CMIP5.png
Nick Stokes: Of course GCMs account for change in solar activity.
The authors note that the spectral density of the sunlight does not remain constant through swings in TSI.
“The solar flux” term as you said is usually used when referring to F10.7cm radio flux, whereas the term you want to use, in conformance with your graphic, is “TSI”. You knew that.
Their TSI graphic has pre-SC19 too low, and SC24 too high. The GISS discussion insinuates the TSI used in CMIP5 is obsolete:
Note this does not yet include updates for the recalibration of the group sunspot number (Clete et al., 2015)
Neither did Lean’s latest paper. From a May 2018 WUWT discussion on that with Leif Svalgaard, I showed past TSI looks more like his and my plots which incorporate the sunspot reconstruction somewhat similarly:
https://www.dropbox.com/s/33e3o3uozb9yscv/Lean%20reconstruction.JPG?dl=0
https://www.dropbox.com/s/myrhxz3012yrrpu/Svalgaard%20vs%20Weber%20TSI%20models.JPG?dl=0
imo, TSI is improperly used in models irregardless of the data used.
…suggesting a measure of predicted luminosity is sufficient to reflect the effects of solar activity on Earth’s climate?
Here is the new empirical finding that provides the ultimate boundary condition for Earth’s global surface temperature https://t.co/SgWzeWz5WE
Have there been any responses to this? According to these calculations the best representation of the temperature of the planets and moons studied is the pressure of the atmosphere, not the composition of it. If this is correct then CO2 is no more a greenhouse gas than O2.
ReLlez spelled backwards is Zeller. I think this particular subject has been pounded into the ground here.
Their leading reference is Volokin and Rellez which is both of them spelled backwards or a major coincidence. What’s up with that? I think they take their readers for fools.
Ned and Karl could not get their work published by consensus alarmist publications because they knew who they were. They published with their names backwards and the stupid publishers did not recognize their names and they found nothing wrong with the material so they published it. Brilliant on Ned and Karl’s part.
I have met and talked to Ned Nikolov* and Karl Zeller in London in 2016, We presented at the same climate conference. Their air pressure is a necessary component of climate, we don’t have climate responses without an atmosphere and more atmosphere can cause more response. They don’t explain the delta temperature changes that don’t depend on just how much air we have. Water and ice on earth do matter and Ned and Karl do not consider that properly. I don’t disagree with what they say, I disagree with what they left out.
” they knew who they were”
Actually, they didn’t. As Nikolov explained, the reason why this subterfuge was needed was that otherwise referees could find where Willis Eschenbach had demolished it at WUWT.
Zeller or ReLlez,
A conjecture about planetary temperatures based exclusively on their atmospheres, disregarding the effect on Earth’s temperature of the oceans and the changes of state of the water molecule cannot be correct.
Besides, your article appears to ignore that the present GMAT of ~14°C is a very temporary situation and that the default GMAT of the Earth over the late Pleistocene is ~10-11°C and that the very important change between both is not mediated by any of the variables you are considering.
I can offer no informed opinion on that paper, because I have previously found the authors’ work unworthy of my time.
But I have not been able to rule out the somewhat-supportive proposition, set forth here: https://motls.blogspot.com/2010/05/hyperventilating-on-venus.html, that beyond a certain optical depth the greenhouse effect on the difference between a planet’s surface temperature and its effective radiation temperature is relatively minor in comparison with the that of the lapse rate caused by rising gas’s adiabatic expansion.
I don’t profess to have vetted that proposition thoroughly, so you may want to compare your interpretation with mine, which is that the effect of the atmosphere’s size on the average surface temperature would still be minimal in the absence of at least some greenhouse effect; it’s just that the returns of the greenhouse effect diminish in favor of the product of the atmosphere’s lapse rate and the altitude of its tropopause.
“I don’t profess to have vetted that proposition thoroughly”
It is a nonsense argument. A lapse rate doesn’t warm anything. It creates a temperature difference across a layer of gas. But the fluxes determine the temperature. If the atmosphere was just N2, the temperature of the surface would be that which radiates the sunlight back to space. If it is assumed the same albedo, that would be cold; less than the snowball Earth 255K.
The N2 doesn’t interact with the radiation. So the temperature is set by the contact with the surface, and just gets colder as you go up. At 92 atmospheres, that is a problem, because soon it would be liquefying. But we’re assuming an ideal gas.
The hot surface of Venus is due to the GHE, not pressure or lapse rate.
I’m perfectly open to a reasoned explanation of why Dr. Motl may be wrong, but I would caution readers against basing such a conclusion on simplistic statements like “A lapse rate doesn’t warm anything.”
Greenhouse gases determine the earth’s effective radiation altitude, but in the troposphere it’s rising air’s adiabatic expansion, not radiative transport. So that expansion principally determines the lapse rate and thus, for a given surface temperature, the temperature at any troposphere altitude, including the effective radiation altitude.
Absent that convection (and any conduction), my guess is that air-source radiation would be a linear function of the optical depth to the air’s altitude. In the actual earth troposphere, the (approximately) linear relationship is instead that between air temperature and altitude.
In other words, the lapse rate affects temperature if greenhouse gases do, so in the absence of a better argument I personally remain open to the possibility that Dr. Motl is right about which of the two influences predominates.
“simplistic statements like “A lapse rate doesn’t warm anything.””
It isn’t a simplistic statement. To warm something, you need a heat source. A lapse rate is just an observed temperature gradient. There is no heat source associated with it as such. You might say that heat always flows along a temperature gradient, but on that simplistic view, the heat flow would be up. In fact, the lapse rate is the outcome that keeps flux in balance. I explain all that here.
“Greenhouse gases determine the earth’s effective radiation altitude”
That part is true, and they in effect shift the point at which temperature is determined, in some wavelengths, from surface to TOA. And you can say that the lapse rate mediates the warming at the surface. But it doesn’t create it. That is where Goddard and Motl go wrong. They say that a lapse rate without GHG would warm (eg N₂). But that is wrong, because there is nothing regulating heat flux at the TOA end.
“In other words, the lapse rate affects temperature if greenhouse gases do”
But the follow-up is that it doesn’t if they don’t.
Just in case there’s some lurker who missed it, I’ll point out that Mr. Stokes is engaging, as is his wont, in high-school-level debating rather than an adult discussion of Dr. Motl’s conclusion: that the majority of the effective-radiation-temperature difference between a planet as a whole and its surface can be determined by lapse rate, with only a minor amount due to the greenhouse effect.
In this case the particular high-school tactic was misrepresenting what Dr. Motl stated as being that “a lapse rate without GHG would warm.” The truth is that Dr. Motl assumed just the opposite; i.e., he assumed that at least some greenhouse gas is necessary.
But one can easily imagine an atmospheric temperature profile not unlike Earth’s in which so increasing the greenhouse-gas concentration as to move the effective radiation altitude through the tropopause could cause no change at all in (dare I say it?) equilibrium surface temperature.
So it masks important complexities to parrot mindlessly that a planet’s effective-radiation-temperature difference is determined mainly by the greenhouse effect.
N2 as a gas doesn’t interact with radiation. On Pluto, the phase change lowers the surface temp 10C.
Pingback: On Boundary Conditions And Initial Values | Transterrestrial Musings
Dan Hughes and Tomas Milanovic, thank you for the essay.
Here is a nice quote from the second linked article: Actually, the concept an equilibrium radiative-energy transport state for Earth’s climate systems is a little fuzzy, and is simply postulated to be attainable at some future time. The future time at which this state will be present is not well defined. Additionally, the time period over which the response metric should be measured in order to verify the hypothesis is also not well defined. It’s all kind of fuzzy.
A SPM published by the IPCC predicted warming over the 1st two decades of the 21st century would average .2 ℃ per decade. The current average over the first 18 years and 5 months of that 20-year timespan is .189 ℃ per decade.
Professor Curry’s firm has forecast an El Niño starting as early as December 2018. As of right now, there is nothing brewing in the Pacific Ocean that would suggest she’s wrong.
Each time a monthly anomaly lands over .82 ℃ GISS, the 30-year trend goes up. They’re likely at the low point of the year, an El Niño will vault the 30-year trend well above .2 ℃.
The IPCC is going to hit a bullseye. What have Hughes and Milanovic hit? I predict sour grapes.
Atmospheric CO2, the control knob of the current regime; heading toward equilibrium:
https://i.imgur.com/IBGzoGf.png
Assume there is a climate equilibrium. What would make one think the GMST measures it?
https://m.imgur.com/BcodSWC
~ graph courtesy of Javier (with a promised update soon)…
This has for consequence that the solutions computed with h(t) as boundary condition are invalid.
For practical purposes, would it not be better to write “inaccurate” for “invalid”, and study the degrees of inaccuracy? Even a “valid” solution computed on a finite-precision machine would entail inaccuracy.
It’s a fine essay.
Re this rather obscure pronouncement: “Importantly, the equations also lead to the requirements that must be met in order for the total energy content to remain constant.”
Total energy content of what? Certainly not volume V or any given subsystem, which is all that have been mentioned up to this point. Their total energy content is highly variable over time (which is what the climate debate is all about). Energy keeps crossing the boundary.
Are you referring to some super system, which in this case might have to be the whole universe? But even there nuclear reactions are constantly creating new energy.
Where then is the total energy content constant?
David Wojick: Where then is the total energy content constant?
They do not claim that energy is constant in the climate system.
Good to know, Matthew, but why then “Importantly”? Have I been distracted by a digression?
Perhaps you can say what they do claim.
David Wojick: Have I been distracted by a digression?
I would not say that. On first reading that sentence seems to imply that they will be getting around to asserting an equilibrium somewhere. Then they become more clearly critical of the idea that the climate system could be in equilibrium.
Or so it seemed to me as I read it.
Reblogged this on Quaerere Propter Vērum.
It is about time that the Western education system recreated itself. It is time we all realize that our schools will remain unfit to do public service until they are divorced from politics.
The previous warm periods (Medieval, Roman and Minoan) likely had the same natural origin as the present one. Hence, we should expect a century of cooling that essentially reverses the warming of the 20th century.
Of course, what has happened will happen again, but the Roman and Medieval warm periods lasted a few hundred years before the cooling. The century of cooling will come later. We warmed because the little ice age ice depleted and retreated. The ice is being replenished now but it takes a few hundred years before there is enough volume and weight to advance and cause the cooling. The solar cycles are small changes that do correlate with temperature changes. The ice extent changes are larger changes that do correlate with larger temperature changes.
Go check the ice cores, it snows more in warm times and it gets cold after.
The Earth is an open thermodynamic system – but that implies a different energy dynamic than thermodynamic equilibrium. The Earth system approaches at an exponential rate a radiative equilibrium at which there is maximum entropy production.
The energy balance of the planet is stark where the climate system meets space. The change in heat energy content of the planet – and the work done in melting ice or vaporizing water – is approximately equal to energy in less energy out. There are minor contributions with heat from inside the planet and the heat of combustion of fossil fuels – for instance – that make it approximate but still precise enough to use. Energy imbalances – the difference between energy in and energy out – result in planetary warming or cooling – and Earth’s strong exponential temperature feedback response tends to drive the planet to a transient energy equilibrium. Maximum entropy is when there is an energy equilibrium at the top of Earth’s atmosphere – energy in equals energy out – and occurs when oceans are neither warming or cooling. The oceans are by far the greatest part of Earth’s energy storage – and the Argo record gives us a real sense of whether the planet is warming or cooling – or both at different times. Some 92% of global heat is in the oceans, 4% in the atmosphere and 4% in latent heat – the latter in liquid water and water vapor.
The global first order differential energy equation can be written as the change in heat in oceans is approximately equal to energy in less energy out at the top of the atmosphere (TOA).
Δ(ocean heat) ≈ energy in – energy out
Satellites measure change in energy in and energy out well but are not so good at absolute values – the inter-calibration problem. But nonetheless CERES has made a stab at balancing the equation. Energy in and out varies all the time. Energy in varies with Earth’s distance from the Sun on an annual basis and with much smaller changes over longer terms due to changes in solar emissions. Outgoing energy varies with cloud, ice, water vapor, dust… – in both shortwave (SW) and infrared (IR) frequencies.
“The top-of-atmosphere (TOA) Earth radiation budget (ERB) is determined from the difference between how much energy is absorbed and emitted by the planet. Climate forcing results in an imbalance in the TOA radiation budget that has direct implications for global climate, but the large natural variability in the Earth’s radiation budget due to fluctuations in atmospheric and ocean dynamics complicates this picture.” https://link.springer.com/article/10.1007/s10712-012-9175-1
The question of how ocean and atmospheric circulation changes emerge and how this influences IR emission and shortwave reflection at TOA over what periods and to what extent is the problem de jour.
Radiative equilibrium appears to happen once a year at least. It is a transient equilibrium that is the best that can be hoped for. This is simply power flux in less power flux out from CERES.
https://watertechbyrie.files.wordpress.com/2018/05/power-flux1.jpg
The average is 0.8W/m2 – consistent with rates of ocean warming. The trend over the period of record is negative. Such large swings in imbalances are not due to greenhouse gases. But there are smaller changes in solar intensity, greenhouse gases and from the fractionally dimensioned state space occupied by the Earth system at some time that are lost in the swings of the boundary energy dynamic.
Climate data at all scales suggest perpetual change as abrupt shifts in state space and persistence in regimes as small changes in TOA radiant flux – both in visible and ultraviolet frequencies it seems – push the system past thresholds. Behavior that is diagnostic of deterministic chaos – temporal or spatio-temporal – common to many systems. The internal response of the system – for which the governing equations do not exist – determine climate change – on which greenhouse gas changes are presumably superimposed and which may themselves push the system past thresholds.
“Finally, Lorenz’s theory of the atmosphere (and ocean) as a chaotic system raises fundamental, but unanswered questions about how much the uncertainties in climate-change projections can be reduced. In 1969, Lorenz [30] wrote: ‘Perhaps we can visualize the day when all of the relevant physical principles will be perfectly known. It may then still not be possible to express these principles as mathematical equations which can be solved by digital computers. We may believe, for example, that the motion of the unsaturated portion of the atmosphere is governed by the Navier–Stokes equations, but to use these equations properly we should have to describe each turbulent eddy—a task far beyond the capacity of the largest computer. We must therefore express the pertinent statistical properties of turbulent eddies as functions of the larger-scale motions. We do not yet know how to do this, nor have we proven that the desired functions exist’. Thirty years later, this problem remains unsolved, and may possibly be unsolvable.” Julia Slingo and Tim Palmer – and it is nearly 50 years now.
Models are very different and there the experiment has been done. Uncertainty in ‘initial’ and ‘boundary’ conditions create non-linear sensitivity. Changes in the breadth and depth of coupling – or even in the order of calculations – provoke structural instability.
“Sensitive dependence and structural instability are humbling twin properties for chaotic dynamical systems, indicating limits about which kinds of questions are theoretically answerable. They echo other famous limitations on scientist’s expectations, namely the undecidability of some propositions within axiomatic mathematical systems (Gödel’s theorem) and the uncomputability of some algorithms due to excessive size of the calculation.” James McWilliams
The practical import is that this results in the evolution of divergent, non-unique solution trajectories in any model.
http://rsta.royalsocietypublishing.org/content/roypta/369/1956/4751/F8.large.jpg
“Schematic of ensemble prediction system on seasonal to decadal time scales based on figure 1, showing (a) the impact of model biases and (b) a changing climate. The uncertainty in the model forecasts arises from both initial condition uncertainty and model uncertainty.”
Here Julia Slingo and Tim Palmer are talking perturbed physics ensembles – and not the opportunistic ensembles of the IPCC. The latter involves an arbitrary choice of solution from many plausible solutions that are then sent to the IPCC and graphed along with other arbitrary choices.
The boundary meme is a misapplication of a linear mathematical idea used to suggest that models will converge on a ‘true’ solution – they do not – or that Earth’s energy budget changes consisting entirely of greenhouse gas forcing will determine the future evolution of climate implying that natural variability is white noise – it is not.
Thank you Robert. Excellent summary. The best bits.
“Energy imbalances – the difference between energy in and energy out – result in planetary warming or cooling –”
“the Argo record gives us a real sense of whether the planet is warming or cooling – or both at different times. Some 92% of global heat is in the oceans, 4% in the atmosphere and 4% in latent heat – the latter in liquid water and water vapor.”
“the change in heat in oceans is approximately equal to energy in less energy out at the top of the atmosphere (TOA).
Δ(ocean heat) ≈ energy in – energy out”
“Energy in varies with Earth’s distance from the Sun on an annual basis and with much smaller changes over longer terms due to changes in solar emissions”
plus the cloud and other albedo effects which also vary energy in
” Outgoing energy varies with cloud, ice, water vapor, dust… – in both shortwave (SW) and infrared (IR) frequencies.”
plus CO2 etc?
“Radiative equilibrium appears to happen once a year at least. It is a transient equilibrium that is the best that can be hoped for.”
Fantastic comment.
I would imagine it happens a lot more than once a year. At the changeover point shown on your graph there would be numerous instances where it goes to equilibrium and out as it goes through the fluctuation. The period of time where this equilibrium can occur many multiple times of short duration is what happens once a year at least.
Some questions. Poor science on my part.
The land gets 30% of the energy in, the oceans 70% so the 92% of global heat in the oceans means none for land?
Most topsoil would have a water component as would vegetation. It implies there is nothing for the land component even though it has a role in heating up 30% of the atmosphere and possibly by a lot more than the ocean during the day and on some cloudy nights.
The lag effect seasonally, like more ice volume keeps forming in the arctic after the longest night even though the energy in is now increasing and more snow on the snow fields suggests there is a delay locally in energy in to energy out for our atmosphere and oceans?
Again there is talk of the lag effect with CO2. I don’t quite get it. If one has 410 ppm CO2 in the atmosphere why is the effect on the atmospheric temperature more or less direct?
Yes some temp will be constantly heating the ocean/land but not enough to take away the temperature that an atmosphere with CO2 at 410 ppm should automatically go to, perhaps with a lag of a minute?
Otherwise, if it does not heat it up by the required amount under the sun’;s forcing that day why do we bother to say it has a greenhouse effect if it refuses to show it?
I got the numbers from James Hansen – so they must be right. But it was the storage of energy and that depends on the density of the medium and the depth of heating so we can pretty much discount the atmosphere from consideration. Land warms by slow diffusion to surprising depths – but cools diurnally and seasonally. But I just accepted the numbers at face value.
If we are talking energy imbalances at toa however – the imbalance must end up instantaneously in the system somewhere. Ocean temperature must co-vary with cumulative power flux imbalances – two very different data series – at toa.
https://watertechbyrie.files.wordpress.com/2018/05/ocean-heat-and-power-flux.jpg
They sort of do – I suspect the early Argo data given warming in net flux (-SW-IR) this century. There appears to be a discrepancy and thus CERES or Argo must be wrong. Nor do I have much confidence in lag due to ocean thermal inertia given the large ocean warming and cooling on an annual basis.
As for the greenhouse effect – it should be there from first principles – and there is evidence from narrow aperture satellite borne instruments that I find convincing. Although how to disentangle this from natural variability is a mystery to me.
https://watertechbyrie.files.wordpress.com/2014/06/harries-2001.png
But in a spatio-temporal deterministic chaotic system we are left with the potential for CO2 to trigger extreme, rapid and adverse shifts – hot or cold – or hydrological – away from relatively benign conditions experienced in the 20th century. Of course that may happen anyway. I don’t want to be alarmist – but I am a catastrophist in the sense of Rene Thom.
Don’t forget other chemical and bio-storage.
RIE, might want to also caveat, CO2 could inhibit such shifts as well.
Just on the CFD bit:
“Fully Verified and Validated commercial-grade CFD software”
CFD worked perfectly well before V&V people got to it.
“Earth’s climate system is vastly more inherently complex than all and any CFD applications because the latter deal uniquely with Navier-Stokes equations”
Complete nonsense. CFD with combustion is a staple. Huge density changes, radiation, probably smoky gases. Shallow water equations. Multi-phase and phase change. Transonic. GCMs are relatively simple, except for the long thin elements. But that can be handled.
“Safety and flight worthiness of commercial aircraft are not functions of any CFD calculations.”
Nonsense. CFD is much used in the design. Of course that affects safety and airworthiness. There are other checks. CFD is used because it yields designs that pass the other checks.
The point about noting CFD is that
1. It shows as false claims that are made about the impossibility of solving Navier-Stokes
2. CFD rejoices in all the chaotic etc issues of GCMs
3. Almost all transient CFD problems share the initial/boundary issues of GCMs described here. Like them, they are solved by time-stepping, so you need an initial state. But the initial state does not numerically determine the states you actually want (chaos). So in both, the initial state is usually placed well away from the solutions of interest, precisely because of the possibility that effects of something non-physical (eg converging flow) will have time to settle down.
The indifference to initial state is numerical, but it reflects the physical. You don’t know the initial state anyway, and you know it doesn’t matter. No-one worries about the initial state when setting up a wind tunnel test. If the result depended on the initial state, that would be the worry, because you certainly don’t know what it would be in flight.
Are you saying CFD’ will be able to accurately determine the impact of man dumping CO2 into the atmosphere? Strikes me as a bridge too far. As Dirty Harry observed, you’ve got to know your limitations.
No. GCMs do that. But all the issues about boundary and initial conditions are present in CFD, as in GCMs.
Although it is arguable that GCMs are CFD. Plenty of CFD has radiation with absorption. Cloud modelling etc makes it a rather specialised CFD.
“Win a million dollars with maths, No. 3: The Navier-Stokes equations
Fluids move in mysterious ways. Mathematicians aren’t even sure the equations that describe them will work in every situation
The Navier-Stokes equations attempt to describe the fiendishly complex movement of fluids. A million dollars in cash (£640,000) awaits anyone who can develop a rigorous mathematical model for how fluids flow – this week’s Millennium Prize Problem”
.And the winner and new millionaire is Nick Stokes
“The point about noting CFD is that It shows as false claims that are made about the impossibility of solving Navier-Stokes”
Put it in and win your million. Go Nick!
I didn’t invent CFD. It has been around for a long time.
Nick Stokes I didn’t invent CFD. It has been around for a long time.”
Nonsense. CFD is much used in the design. Of course that affects safety and airworthiness. There are other checks. CFD is used because it yields designs that pass the other checks.
Safety and flight worthiness were assessed for decades before CFD got involved. CFD does not yield designs. People yield designs.
Yes – it seemed like putting the computer before the wind tunnel.
Which they do.
Nick, Be careful here.
First safety of aircraft is verified using very long flight testing campaigns. In reality, the design is done using only a few flight conditions. The rest are assumed to be OK. Usually that works but there have been problems in flight test for example the 747-8. The main elements of structural design still require test data to set things like lift curve slopes.
Second, wind tunnel testing in fact uses continuation in angle of attack. You start at a benign and low alpha and then gradually increase it. Initial conditions do sometimes matter as recent papers show. Look for “numerical evidence of multiple solutions for the reynolds’ averaged navies stokes equations.”
Wow. This post shows an astonishing amount of arrogance and shows exactly why the climate models need to be under the curatorship of mathematicans, not a bunch of amateurs.
Climate science will never progress while people who have absolutely no understanding, nor respect for the inherent difficulties (impossibilities?) of numerical modelling are at the helm.
“the climate models need to be under the curatorship of mathematicans, not a bunch of amateurs.”
I am not a curator of climate models. But I know how it works. I am a mathematician, and I am not an amateur in numerical modelling. I wrote CFD programs that worked. And you?
So let us analyse what transpired. Don Hughes reported that CFD is, essentially, an incredibly difficult field, and that, modelling in CFD is a very inexact and very imprecise business. He also pointed out that the extra complexities that climate adds to the simple CFD model make the use of the reputation of CFD even less relevant. He warned quite strongly against using the various successes in CFD as some kind of proof that GCM’s share in any of that success.
You treated these sentiment as laughable, and proceeded in a pathetic attempt to get past Dan’s concern vis chutzpah, i.e., these problems do not exist because I called them nonsense and said so.
Whatever.
Climate science is rife with chutzpah and the esoteric/exoteric nonsense, whereby long, muddled ramblings are use to obfuscate the obvious issues that completely invalidate the conclusions. This is the typical technique of the ideologues, and it proves, if anything, that climate science is, in fact, not science at all, but ideological garbage.
I’ve seen people spend years simulating fluid in a 3×3 inch cavity with little to no results of accuracy, but you insist that computing the results in the entire world are ‘handled’. To use a more creative phrase than your own, ‘balderdash’.
This entire sentiment of over confidence shows your lack of understand about numerical errors, modelling errors, stability issues, etc… etc…. The fact you are a ‘mathematician’ is great, it shows some college got funding, but it is obvious from your statement that your training in the area of numerical simulation is not of any standard that would qualify you as ‘expert’, despite what your own ego might be telling you.
As for me, I was trained by a world class expert in the solution of numerical differential equations, with focus on numerical and modelling error, i.e. the limits of such solutions, and the means with which to analyse such things. But that isn’t really relevant, is it, because I am not the one claiming to solve climate models and misleading both lawmakers and policy makers with a bunch of baloney, right? And I have the good sense not to work in field full of imposters like yourself who have no interest in the accuracy/limitation of such solutions.
Besides, the pay sucks.
Wow. Just wow.
Truly medieval.
I guess the takeaway here is that education, especially in climate modelling needs a seismic shift. The fields of error analysis, numerical error analysis need a major boost. Mathematics needs to take its place in the climate science institutions.
But math alone certainly can make no progress. True interdisciplinary dialogue needs to find a path to expression. Which is difficult. Nobody likes the math guys. We stop the fantasies and it annoys people.
The alternative is this sort of overconfidence leads the field into irrelevance and mockery.
But, of course, that is unlikely to happen in the failing west that can’t even keep its roads level. No one cares about results. It’s only all about the ideology. And, science, from the start, has been a tool of the elites, not the truth.
OK, there’s more
“In this regard, GCMs using the hydrostatic approximation represent ILL-Posed Initial-Boundary Value Problems.”
All CFD, with or without hydrostatic approximation, is ill-posed, on this definition.
“A boundary of a physical 3D system is necessarily a surface so giving a boundary condition means to prescribe the value of the unknown functions for every point and every time at this surface.”
No, it doesn’t. It means prescribing some constraint, probably expressing continuous boundary stress. On land, this mostly is zero fluid velocity at the surface, although there will generally be a special boundary model (wall function), because velocity gradients near the surface are too fast to fit with the grid approximation. Over sea, there will e a complicated model which not only keeps stress across the boundary continuous, but allows for heat and gas exchange, evaporation etc. But you don’t generally have to prescribe values, just relations.
At TOA there is zero boundary stress, although the formulation needs to be flexible enough to allow gravity waves.
“The second is not a boundary condition”
Easterbrook didn’t say it was. He merely said we have to worry about boundary values. Not specify them.
“Lorenz was able to show that even for a simple set of nonlinear equations (1.1), the evolution of the solution could be changed by minute perturbations to the initial conditions, in other words, beyond a certain forecast lead time, there is no longer a single, deterministic solution and hence all forecasts must be treated as probabilistic. The fractionally dimensioned space occupied by the trajectories of the solutions of these nonlinear equations became known as the Lorenz attractor (figure 1), which suggests that nonlinear systems, such as the atmosphere, may exhibit regime-like structures that are, although fully deterministic, subject to abrupt and seemingly random change.” http://rsta.royalsocietypublishing.org/content/369/1956/4751
It applies as much to Lorenz’s simple nonlinear equations as climate models. Nick resists mightily but seems to mightily and persistently miss the point. The experiment has been done – and even with a constrained solution space the spread of solutions given realistically assessed imprecision in input parameters is wider than IPCC opportunisitc ensembles. The best that can realistically be extracted from climate models as climate forecasts are probability distribution functions at seasonal to – perhaps – decadal scales. The rest is scientific nonsense.
https://watertechbyrie.files.wordpress.com/2018/05/rowlands-2012.jpg
https://www.nature.com/articles/ngeo1430
This is not a matter of empty waffle about CFD – but a demonstrated mathematical reality in blue and white.
Like Dr Johnson – I am a simple soul.
http://www.willfawke.co.uk/images/commisioned-statues/large056.jpg
“but seems to mightily and persistently miss the point”
No, that is your role. Firstly, again, exactly the same situation applies in CFD, and that is major engineering. You can’t track trajectories reproducibly, but you can track mean flow and derive the key flow properties, like lift and drag for an aircraft wing. You don’t care what tracks fluid elements followed, because inter alia you didn’t know where they were in the first place. If it mattered you’d be stuft. But it doesn’t.
And the same with GCMs. You can’t track weather reproducibly. But you can reproduce the evolution of climate averages in response to forcing changes.
Weather forecasts can’t track weather reliably for the the same reason that climate models don’t track climate – increasingly common are probabilistic forecasts for weather, for ENSO and for seasonal to decadal climate forecasts. Conceptually – the many solutions sample the model state space. Practically these many plausible solutions do not track the evolution of climate but at most can suggest the probability of outcomes within a diverging range. Models may provide statistics of the model state space but not forecasts
This has been said again and again by leaders in the field and demonstrated conclusively by actually running perturbed physics ensembles. As I say the experiment has been done.
Climate like turbulent flows evolves chaotically – but it is as stated not confined to fluid dynamics – but includes cloud, ice, dust, biology as well as chaotic oscillators in ocean and atmospheric circulation at all scales.
Your resistance to understanding this is both astonishing and anticipated.
“In sum, a strategy must recognise what is possible. In climate research and modelling, we should recognise that we are dealing with a coupled non-linear chaotic system, and therefore that the long-term prediction of future climate states is not possible. The most we can expect to achieve is the prediction of the probability distribution of the system’s future possible states by the generation of ensembles of model solutions. This reduces climate change to the discernment of significant differences in the statistics of such ensembles. The generation of such model ensembles will require the dedication of greatly increased computer resources and the application of new methods of model diagnosis. Addressing adequately the statistical nature of climate is computationally intensive, but such statistical information is essential.” IPCC TAR 14.2.2.2
“but a demonstrated mathematical reality in blue and white”
But reality of what? It just says that spread increases as you go on in time. And it’s real; it represents the growth of entropy. You can’t avoid that.
What does the graph look like? A plume from a smoke stack in a steady breeze. It isn’t a numerical artefact; it really happens.You can’t pin things down as well in 2100 as in 2050. That’s life.
It is clear that the many feasible solutions of models evolve from sensitive dependence on initial conditions. That was the entire point of the large perturbed physics ensemble.
This is one of those theories that has no rational grounds for objection. And comparing models to smoke and paint misses the point entirely.
http://www.pnas.org/content/pnas/104/21/8709/F1.large.jpg
“Generic behaviors for chaotic dynamical systems with dependent variables ξ(t) and η(t). (Left) Sensitive dependence. Small changes in initial or boundary conditions imply limited predictability with (Lyapunov) exponential growth in phase differences. (Right) Structural instability. Small changes in model formulation alter the long-time probability distribution function (PDF) (i.e., the attractor).”
http://www.pnas.org/content/104/21/8709
You are so very clearly misguided. Here’s a comment from above in case you missed it.
https://judithcurry.com/2018/06/25/of-boundary-and-initial-conditions/#comment-875449
But I don’t really think I could put a dint in your agnotology.
Nick,
The focus is on GCMs, and evolving ESMs. More explicitly, the energy content and especially radiative energy transport, in both the mathematical and physical domains. The post ends with this:
Here’s the Question
Within the framework of GCMs and all other factors summarized above,
(1) identify the boundaries of the physical domain that are represented in GCMs, e.g define the surface B which constitutes the invariant boundary of the whole system under study.
(2) describe the Boundary Condition(s) (BCs) that are imposed on the boundary, and
(3) describe the equation(s) and dependent variable(s) to which each BC that applies at the boundary B, e.g prescribe explicitely N functions Gi(x,t) defined on B such as for all dynamical parameters Fi(x,t) defined on B we have Fi(x,t) = Gi(x,t) for all x included in B.
Suggest a mechanism allowing to obtain a unique solution of the dynamical equations depending only on the boundary conditions and justify the time scale T at which this mechanism would start to operate.
Dan
“Here’s the Question”
Well, the answer is simply what they do. Here is the math description of CAM 3. Basically you have to do all that to make a pde process work. And it does.
I don’t know what you mean by an invariant boundary, but the actual boundaries are clear. GCMs use topographic coordinates to follow terrain. Boundary conditions are variations of continuous stress. At land surface, that means zero velocity, at sea bottom too. At TOA it is basically zero stress – hydrostatic constant with no horizontal acceleration. At the sea surface, it is continuity of fluxes and stress. In boundary layers, special sub-grid treatment may be needed (wall functions).
ok, I’ll try one more time.
“The focus is on GCMs, and evolving ESMs. More explicitly, the energy content and especially radiative energy transport, in both the mathematical and physical domains.”
Easterbrook didn’t say it was. He merely said we have to worry about boundary values. Not specify them.
Gonna be kind of difficult getting unique solutions to PDEs by only worrying about BCs and not specifying them.
You need to specify boundary relations. Not necessarily boundary values.
As I recall, energy flux is ill defined, depending in particular on the coordinate system. The example is a motor belt crossing a surface. Which side of the belt is moving depends on the coordinate system movement. The moving half carries the energy.
“The dynamics make a big difference in the overall energy balance and are chaotic. Thus feedbacks mediated by these dynamics are critical to determining the effect of the forcings..”
Ocean dynamics are the negative feedbacks to forcings. During deeper solar minima episodes, El Nino episodes roughly double in frequency, and the AMO is in its warm phase. Calling them chaotic or ‘internal variability’ only illustrates a lack of knowledge of their nature, and negates the means of usefully predicting climate change.
“While these short term fluctuations are indeed chaotic and lead to the unpredictability of the weather which is the base on which the climate is defined”
A circular logic which should on average yield no climate change. No they are not indeed chaotic, the North Atlantic and Arctic Oscillations are strongly effected by solar wind variability in the short term. And there are means to predict it.
And yet the world warms, sea levels rise, CO2 increases, nights warm faster than days, stratosphere cools…
Some things are easy to monitor. These were predicted. No need to muddy the waters.
Yet there remains all sorts of thing to astonish and amaze.
https://watertechbyrie.files.wordpress.com/2016/02/sst_anomaly_amsre_2008105.jpg
Unlike El Niño and La Niña, which may occur every 3 to 7 years and last from 6 to 18 months, the PDO can remain in the same phase for 20 to 30 years. The shift in the PDO can have significant implications for global climate, affecting Pacific and Atlantic hurricane activity, droughts and flooding around the Pacific basin, the productivity of marine ecosystems, and global land temperature patterns. #8220;This multi-year Pacific Decadal Oscillation ‘cool’ trend can intensify La Niña or diminish El Niño impacts around the Pacific basin,” said Bill Patzert, an oceanographer and climatologist at NASA’s Jet Propulsion Laboratory, Pasadena, Calif. “The persistence of this large-scale pattern [in 2008] tells us there is much more than an isolated La Niña occurring in the Pacific Ocean.”
Natural, large-scale climate patterns like the PDO and El Niño-La Niña are superimposed on global warming caused by increasing concentrations of greenhouse gases and landscape changes like deforestation. According to Josh Willis, JPL oceanographer and climate scientist, “These natural climate phenomena can sometimes hide global warming caused by human activities. Or they can have the opposite effect of accentuating it.”
As I said above – the question of how ocean and atmospheric circulation changes emerge and how this influences IR emission and SW reflection at TOA over what periods and to what extent is the problem de jour. It is possibly too late – the waters are very turbulent.
And in spite of the smaller wheels, we turn the big wheel.
The extra warming is not coming from the sun.
Warming and cooling results from deterministic chaotic shifts in ocean and atmospheric circulation in coupled ocean/atmosphere processes.
https://www.facebook.com/Australian.Iriai/posts/1608494905933432
The Pacific is a pretty big wheel.
https://i.imgur.com/yvrMXFy.png
(the sun is a pretty big wheel, too)…
Over millennia. It is not white noise. That is the point.
https://watertechbyrie.files.wordpress.com/2017/12/moy-2002-wavelet1.jpg
“Since “panta rhei” was pronounced by Heraclitus, hydrology and the objects it studies, such as rivers and lakes, have offered grounds to observe and understand change and flux. Change occurs on all time scales, from minute to geological, but our limited senses and life span, as well as the short time window of instrumental observations, restrict our perception to the most apparent daily to yearly variations. As a result, our typical modelling practices assume that natural changes are just a short-term “noise” superimposed on the daily and annual cycles in a scene that is static and invariant in the long run. According to this perception, only an exceptional and extraordinary forcing can produce a long-term change. The hydrologist H.E. Hurst, studying the long flow records of the Nile and other geophysical time series, was the first to observe a natural behaviour, named after him, related to multi-scale change, as well as its implications in engineering designs. Essentially, this behaviour manifests that long-term changes are much more frequent and intense than commonly perceived and, simultaneously, that the future states are much more uncertain and unpredictable on long time horizons than implied by standard approaches. Surprisingly, however, the implications of multi-scale change have not been assimilated in geophysical sciences. A change of perspective is thus needed, in which change and uncertainty are essential parts.” https://www.tandfonline.com/doi/abs/10.1080/02626667.2013.804626
https://watertechbyrie.files.wordpress.com/2018/05/nile-e1527722953992.jpg
Structured random is Greek for deterministic chaos. Data says chaos and if ones eyes are attuned chaos if everywhere.
Interminably repeating simplistic memes – as both sides do – leads nowhere interesting.
So Ellison thinks the Pacific is the source of heat.
Never explains how or why. Just that the Pacific is the source.
How is it the biggest wheel? It moves heat around. It does not produce heat.
“Having comprehensively stuffed this up”
I believe you really did stuff this up. But you never tell us where the warming is coming from. Hint: moving heat around is not adding heat.
Go back to the big picture of open and closed cell cloud from Rayleigh–Bénard convection and try to to understand something. Rather than behaving like an ignorant and ill mannered lout.
2100.
Abrupt climate change is rare. Your bet is foolhardy.
Abrupt climate change is rare
So how does that refute the luke warmer position that indeed we are experiencing climate change, but natural variability is padding the total? (and we don’t actually know what percentage of the warming is natural vs anthropogenic?)…
https://watertechbyrie.files.wordpress.com/2014/06/vance2012-antartica-law-dome-ice-cores-salt-content.jpg
~ graph courtesy of robert
The thinking goes that long term changes in enso affect cloud cover. (therefore, natural internal variability can create climate change all on its own)…
https://watertechbyrie.files.wordpress.com/2014/06/vance2012-antartica-law-dome-ice-core-salt-content.jpg
“But you never tell us where the warming is coming from. Hint: moving heat around is not adding heat.”
Moving heat into the oceans (92%) and deeper than the sea surface impacts the GMST. So do we just refer to the GMST or the system total as we want? Moving heat around is what my Ranger does with its engine cooling system. Moving heat around fits nicely with the idea of an equilibrium. Moving heat around in my opinion is joules leaving at the TOA. Adding insulation will warm. But if one only understands the insulation and say 60% of the system, how much warming is nicely summarized by the IPCC with its banner statement on ECS.
We might also say, Moving heat around is not subtracting heat. Movement has nothing to do with total heat. Moving heat to a certain latitude with the Milankovitch cycle, nada.
Moving heat from the ice on land in Antarctica, also nada. Moving heat into the form of water vapor rather than ocean water, also nada.
‘No need to muddy the waters.”
Mother Nature muddied the waters by making the planet Earth so gosh darn complicated. Glacial and interglacials, land drifting, rising and sinking. Ocean currents, wind patterns, ice, vegetation and volcanoes.
Mother Nature made the earth climate self correcting such that it deals with orbit and tilt changes, solar cycle changes, human contributions, etc.
Mother Nature don’t care what we do, she takes care of business of climate control and keeps earth in narrow bounds. The past 50 million years have been inside a 20 degree range. The last 5 million years have been inside a 10 degree range and the past 10 thousand years have been inside a 4 degree range and not headed out.
And yet, we warm. Some climate are easy watch unfold. Just because you put wheels inside of wheels does not mean that we won’t have seasonal climate change or continue to warm each decade because of CO2.
It appears that this site is still sticking to “it’s complicated, so we can’t be warming the earth.”
Sure it warmed – all in the tropics it seems.
https://watertechbyrie.files.wordpress.com/2017/11/argo-e1512162547947.jpg
But the question is why and grossly oversimplifying dynamic complexity is the governing silliness.
https://watertechbyrie.files.wordpress.com/2018/05/ceres_ebaf-toa_ed4-0_anom_toa_longwave_flux-all-sky_march-2000tonovember-2017.png
That’s cooling in SW and warming in IR – btw. Now do us all a favour and go away – the adults are talking.
https://watertechbyrie.files.wordpress.com/2018/04/ceres_ebaf-toa_ed4-0_anom_toa_shortwave_flux-all-sky_march-2000toseptember-2017.png
Having comprehensively stuffed this up – I think I’ll go away.
That is of course warming in SW and cooling in IR.
This is what I wrote :
These oscillations illustrate that it is not only impossible to predict their dynamics but it is also impossible to predict probabilities that this or that particular event takes place.
And this is what somebody wrote :
The ice core data explains ice ages and they are not chaotic. A sufficient supply of warm ocean water in cold places will lead to a major ice age because there is an ample supply of water and energy to produce an ample supply of ice.
The person obviously didn’t understand what I wrote . I was not saying that ice ages are not (qualitatively) explained . The Milankovitch cycles are a good candidate for an explanation .
What I wrote was that they cannot be predicted what is a completely different thing .
I am not aware that anybody predicted the next ice age , its duration and its dynamics . This is precisely what chaos theory (or non linear dynamics which is a synonyme) does for you . The Lorenz system is very well explained . We know why it does what it does . But we know it only once it has been done – it is not predictable . Or like the saying goes – predicting the past is easy, predicting the future is generally more difficult .
Past climate cycles have repeated in the same range for ten thousand years. An accurate prediction for the next ten thousand years is that it will continue inside the same bounds in similar cycles.
I have predicted the next ice age, its onset and duration and its dynamics will be similar to the little ice ages of the recent ten thousand years. We will stay warm in this warm period a few hundred years, much like past recent warm periods and then it will get cold. The next ice age will be another little ice age, we only have enough excess ocean water to form ice for a little ice age.
it is also impossible to predict probabilities that this or that particular event takes place
The probability of the next little ice age is 100%, cold periods have always followed warm periods. Nothing has changed to stop what has always happened.
What I wrote was that they cannot be predicted what is a completely different thing .
When there is ample warm thawed ocean available, ice ages will happen.
Energy in, ample water for evaporation and ample IR out = ice age follows
But we know it only once it has been done – it is not predictable
Once it has done the same thing for ten thousand years, it is predictable.
Somebody wrote a few interesting things which ask more questions than they give answers all the while violating about every correct definition what was precisely among others our topic :
The article discounts the value of the energy balance too easily There is an energy balance equation, but it is not Qin=Qout, it is Qin-Qout=Imbalance. Over periods of 30 years or so, an imbalance of only 1 W/m2 is easily measurable as a gain in heat content even though Qin and Qout are individually hundreds of times larger. The fact that there is an imbalance means that there is also an equilibrium state where the imbalance is zero.
– Where is exactly the Qin and Qout defined ? I assume that it is a sphere . What is its diameter ? How is it made sure of that Pin and Pout is known on every point of the sphere for a given t ? (I remind that what we can measure is power and energy is deduced from there by integrating over the whole surface of the sphere) . This is what means the Gauss’ theorem .
– If there is an imbalance it just means that there is an imbalance . And as there is an imbalance at every t and every x , then there is imbalance everywhere and for all times . If Imbalance = 0 it never meant that there is any kind of equilibrium . It just means that the total energy of the system is constant but the dynamics are still as chaotic as they were when imbalanc =/= 0 . Just read the post – a spherical body exchanging radiation with a source is never in equilibrium regardless of any irrelevant imbalances . At best in a steady state .
– Eventually after the forcing stops changing, the response (usually defined in terms of the mean surface temperature) catches up and the imbalance goes away. That is the new equilibrium.
No there is no equilibrium . There cannot be . I think that we clearly explained that the dynamics of the system (I guess it is what is meant by “response”) do not, repeat do not, reach any kind of equilibrium regardless of what happens at some arbitrary and still not specified boundary .
Whether you want to call a forcing change a boundary value problem is semantics. The reality is that the climate is specified by the forcing, and climate change is dominated by the forcing change.
We do mathematics not semantics . The person probably never took PDE lessons . Try to say to the mathematics professor that boundary and initial conditions are semantics and don’t matter for the dynamics . The phrase above is a kind of meaningless mantra which makes mathematically no sense for the system under study and would get a grade F in introductory course of PDE .
Tomas Milanovic: Somebody wrote a few interesting things which ask more questions than they give answers all the while violating about every correct definition what was precisely among others our topic :
Thank you for your follow-up comments.
It’s cross purposes because the earth’s energy budget (Qin-Qout=Imbalance) does use Gauss’s theorem, and they don’t seem to have realized that yet. This is why the Imbalance is also the energy gain of the earth itself, mostly the ocean heat content gain. It can be expressed as Qin-Qout=dH/dt where H is the heat content.
Tomas: As a pragmatist, a billion years of geological history is enough to convince me that the climate feedback parameter for our planet is “always” negative: Despite chaos, the change in the sum of LWR emitted and SWR reflected will always be negative (more heat lost) as average temperature rises. This means there has been no runaway greenhouse (and that I don’t need to worry about one). A negative climate feedback parameter implies that q_out will tend to approach q_in and produce a meaningful steady state (despite small chaotic fluctuations from the mean).
However, since many discuss the possibility of a runaway greenhouse effect, I believe they are unconsciously admitting the existence “alternative Earths” and AOGCMs where a steady state doesn’t exist and chaos reigns. Likewise, the sudden shifts in the climate in Greenland during the last ice age (DO events) prove that regional climate can behave chaotically. The course of the last termination also appears chaotic: gradual warming in Antarctica; delayed and then rapid warming in Greenland, followed by the Younger Dryas and final warming. These observations and arguments appear to refute the position of your critics.
The orbits of the planets around the sun are chaotic, but I don’t worry about the remote possibility the Earth’s orbit will be seriously perturbed in the coming century. 10 millennia of the Holocene provide a reasonable estimate of the unforced climate variability our planet will experience over the next century or two. During this period, a steady state has dominated. I see no reason to worry about either chaos in either situation simply because the equations for both situations admit chaotic solutions.
Should forced warming from rising GHG’s cause me abandon my complacency about unforced variability in the next century or two?
Chaotic fluctuations in currents transferring heat between the surface and deep ocean are likely the source of the largest unforced variability in our climate. As the planet warms, the ocean will become more stably stratified, reducing the likelihood of such chaos. (If the planet were cooling, the opposite would be true.) The melting of ice caps also makes the ocean more stably stratified. Is there anything about a WARMING planet that would make it more susceptible to unforced variability?
Integrate the Planck radiation formula over wavelength and you get the Stefan-Boltznmann law that says that radiated power from a blackbody is proportional to T^4. Although Earth is not a blackbody – the principle applies.
http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/Planckapp.html#c1
And deterministic chaos is the fundamental mode of climate change.
https://watertechbyrie.com/2014/06/23/the-unstable-math-of-michael-ghils-climate-sensitivity/
“Recent scientific evidence shows that major and widespread climate changes have occurred with startling speed. For example, roughly half the north Atlantic warming since the last ice age was achieved in only a decade, and it was accompanied by significant climatic changes across most of the globe. Similar events, including local warmings as large as 16°C, occurred repeatedly during the slide into and climb out of the last ice age. Human civilizations arose after those extreme, global ice-age climate jumps. Severe droughts and other regional climate events during the current warm period have shown similar tendencies of abrupt onset and great persistence, often with adverse effects on societies.” https://www.nap.edu/read/10136/chapter/2
Climate shifts at decadal scales – due in the next decade – and that may be the most pertinent factor for 21st century climate and society.
“– Where is exactly the Qin and Qout defined ? I assume that it is a sphere . What is its diameter ?”
–
Sorry to nit pick. Due to the uneven shape of the earth, it’s rotation and the irregular gravity composition plus different air pressures and night and day changes the TOA resembles an irregular partly deflated basketball. In rotation. At any one time T=0 your boundary condition is met but there is complex change getting to T=1 and beyond.
–
An interesting point is that despite all this the earth does reach transient equlibrium/s when the sun changes from close to far in its orbit with a lag of course. I would have thought this would be twice a year, not at least once a year but never mind.
–
This of course could act as locus for T=x events to help delineate equations for the system since the new system is in balance like the old system though the total mass/volume dynamic is unlikely to ever be quite the same.
Perhaps the energy level and timing of these crossovers could help improve Judith’s Hurricane forecasts both as to start date and possible intensity.
Qin and Qout are defined on a sphere and measured by satellites. This is a well defined concept: integration of energy flux through a spherical surface, both in physics and mathematics. The inward part is direct solar, and the outward part is reflected solar plus emitted longwave. If these integrated values don’t cancel out, there is an imbalance, which means an accumulation or loss of energy within that sphere. Not only that, but this accumulation or deficit is measurable even if it averages ~1 W/m2 for a few decades. Most of the storage, for reasons of heat capacity, ends up being in the oceans, and the Argo measurements have sufficient accuracy to quantify the energy gain rate or imbalance. So when I say Qin-Qout=Imbalance, I am referring to integrated energy fluxes across a spherical surface and the energy total within that sphere. Currently Qin>Qout and this is the measured imbalance that stands at ~0.7 W/m2 currently. The energy budget can either be done by satellites measuring the TOA radiative flux components or via the ocean heat content change. Both show a significantly positive imbalance that matches within observation errors. Equilibrium would be an energy balance, Qin=Qout. Currently the imbalance is positive meaning we are below the equilibrium energy content required to make Qout (emitted longwave) large enough to match Qin, so more warming is in the pipeline until we get to that level.
Energy conservation is a guiding principle. If you’re not considering the long-term energy budget, you’re doing something wrong. If Qin > Qout, that heat is going into the heat content. If you suppress Qout, that increases the heat content.
And the rambling goes on . Energy conservation is a law That’s taken care of by the Gauss theorem . Period .
However there is another dramatic mistake .
Energy is not heat and heat is not conserved . While energy is conserved not only in the long-term but forever, heat isn’t .
Gauss’ theorem doesn’t apply to heat .
QED .
The budget is the integrated energy flux through a spherical surface leading to a net gain/loss of total energy in the interior. This is about as well defined as an energy budget can be, and these fluxes and gain are measurable agreeing with each other on the sign of the imbalance. Mathematically this is Gauss’s theorem applied to energy.
dpy6629 said :
JimD, Energy balance methods are perfectly valid. The problem here is that you need to know the outgoing energy to use them and that outgoing energy is a result of the chaotic dynamics of the system.
Yes, you perfectly got it dpy . This is what mathematics and physics say .
Now that Tomas has provided a concise summary, including explicit specification of at least one of the boundaries, let’s get a little more specific about the main issue.
The previous post at Climate Etc. resulted in lots of interesting discussions. The current post was constructed to address the following statements that arose in those discussions.
(1) What they know is that regardless of any amount of turbulance or chaos in the fluid flow, that overall, and globally, the final state is limited by boundary conditions.
(2) The boundary values are the conditions that constrain the climate over the long-term and are things like how much energy we get from the Sun, how much is reflected back into space, how much energy is radiated from the surface, and how much of this escapes into space. The latter depends on the composition of the atmosphere, and so this is often more associated with a boundary value, rather than being regarded as an initial value.
A key point is that the system will always tend towards a state in which the amount of energy coming in, matches the amount going out into space, and that this state depends mostly on the boundary conditions. This quasi-equilibrium state will then set things like the surface temperatures, latitudonal temperature gradients, large-scale circulation patterns, and how much energy is in the system. Hence, it will determine the typical properties of the climate.
Several others, all fully consistent with those quoted here, are present, but these two provide focus.
On a top-down approach, we’re looking for explicit mathematical descriptions of those BCs, and explicit definitions of where on the boundaries these boundary conditions/constraints/values are located.
The mechanisms by which the explicitly identified and located BCs accomplish the outcomes stated in the above quotes is also of interest. The outcomes can be summarized as follows:
“. . . the final state is limited by boundary conditions.”
“The boundary values are the conditions that constrain the climate over the long-term . . . ”
“. . . and that this state depends mostly on the boundary conditions.”
Our closing summary in the current post was specifically and purposefully stated within the framework of the mathematics and physical domains that were the subjects of the post. The summary also requested additional information about the BCs.
Here’s the Question Within the framework of GCMs and all other factors summarized above,
(1) identify the boundaries of the physical domain that are represented in GCMs, e.g define the surface B which constitutes the invariant boundary of the whole system under study.
(2) describe the Boundary Condition(s) (BCs) that are imposed on the boundary, and
(3) describe the equation(s) and dependent variable(s) to which each BC that applies at the boundary B, e.g prescribe explicitely N functions Gi(x,t) defined on B such as for all dynamical parameters Fi(x,t) defined on B we have Fi(x,t) = Gi(x,t) for all x included in B.
Suggest a mechanism allowing to obtain a unique solution of the dynamical equations depending only on the boundary conditions and justify the time scale T at which this mechanism would start to operate.
Physics and mathematics successfully function only so long as an established and universally accepted nomenclature is honored.
oops, landed in the wrong place. maybe a moderator can annihilate this one.
Unfortunately I have not the time to answer on every comment . I tried to read them all and selected only a few of the most absurd or wrong if you wish.
The last jewel is the following . Also here it is hard to pack as many irrelevant nonsense in only few sentences :
We said :
“A boundary of a physical 3D system is necessarily a surface so giving a boundary condition means to prescribe the value of the unknown functions for every point and every time at this surface.”
Somebody said :
“No, it doesn’t. It means prescribing some constraint, probably expressing continuous boundary stress. On land, this mostly is zero fluid velocity at the surface, although there will generally be a special boundary model (wall function), because velocity gradients near the surface are too fast to fit with the grid approximation. Over sea, there will e a complicated model which not only keeps stress across the boundary continuous, but allows for heat and gas exchange, evaporation etc. But you don’t generally have to prescribe values, just relations
I will be simple so that even readers with little to no knowledge of partial differential equations like the person quoted can understand .
In a physical system with 3 spatial dimensions governed by a PDE we look for an unknown function u(x,y,z,t) which will give us the dynamics of the system for every time and in all space points where the PDE is valid .
First we need to know where u(x,y,z,t) lives . It is generally NOT the whole space but an open subset U of the whole space (imagine for example a sphere) and the system studied is what is inside the sphere where the PDE is valid .
So u(x,y,z,t) is such as for (x,y,z,t) in U x R+ ->u(x,y,z,t) in R^n .
What is the boundary of an open ball ? The surface of the ball !
So now we defined uniquely and unambiguously that the boundary of the system is the surface of the sphere . Everybody with me ?
Second why do we bother ?
Well the PDE theory is telling us that the PDE alone has an infinite number of arbitrary functions for solutions . You will agree that if we want to know what the system will do and where, an answer of the kind “whatever you want” is not interesting .
Fortunately the same theory is telling us that in some cases IF we specify boundary and/or initial conditions the PDE has a unique solution in U .
This is why we bother . Still here ?
Third what is then a boundary condition and an initial condition ?
Well the boundary condition is the value of u(Xb,Yb,Zb,t) (or of its derivatives but I won’t complicate) on the boundary which, as you remember, is the sphere surface . That is why the coordinates Xb,Yb,Zb are coordinates of points that are all on the surface of the sphere .
Finaly a boundary condition is : u(Xb,Yb,Zb,t) = g(Xb,Yb,Zb,t) where g is any function you want but needs only be defined on the surface of the sphere .
How do you translate the equation above in words ?
“Giving a boundary condition means to prescribe the value of the unknown function u to be equal to a GIVEN function g defined on the boundary” what is exactly what we said .
Everybody follows ?
Now compare the correct statement above with the statement of the quoted person : “No it doesn’t” :) Does somebody think that this person understood whatsoever about what we wrote ? I Don’t .
I could add that a bit later the person is talking about “grids” which have nothing to do with the exact mathematical theory but with numerical approximations which are irrelevant .
Last what is an initial condition ? Only fast because topologically it is the same thing as a boundary condition .
Here we impose that u(x,y,z,0) = h(x,y,z) . It just means that instead of considering a spatial boundary (a sphere surface) we consider the boundary of time which is by convention 0 (the initial time t=0) .
Thus it means that we prescribe that u(x,y,z,t) must be equal to the value of some arbitrary function depending only on space h(x,y,z) everywhere inside the sphere but only for time t=0 . It is simple common sense – if you don’t know where you start you won’t know where you’ll be in 1 second or in 1 hour ..
Now that Tomas has provided a concise summary, including explicit specification of at least one of the boundaries, let’s get a little more specific about the main issue.
The previous post at Climate Etc. resulted in lots of interesting discussions. The current post was constructed to address the following statements that arose in those discussions.
(1) What they know is that regardless of any amount of turbulance or chaos in the fluid flow, that overall, and globally, the final state is limited by boundary conditions.
(2) The boundary values are the conditions that constrain the climate over the long-term and are things like how much energy we get from the Sun, how much is reflected back into space, how much energy is radiated from the surface, and how much of this escapes into space. The latter depends on the composition of the atmosphere, and so this is often more associated with a boundary value, rather than being regarded as an initial value.
A key point is that the system will always tend towards a state in which the amount of energy coming in, matches the amount going out into space, and that this state depends mostly on the boundary conditions. This quasi-equilibrium state will then set things like the surface temperatures, latitudonal temperature gradients, large-scale circulation patterns, and how much energy is in the system. Hence, it will determine the typical properties of the climate.
Several others, all fully consistent with those quoted here, are present, but these two provide focus.
On a top-down approach, we’re looking for explicit mathematical descriptions of those BCs, and explicit definitions of where on the boundaries these boundary conditions/constraints/values are located.
The mechanisms by which the explicitly identified and located BCs accomplish the outcomes stated in the above quotes is also of interest. The outcomes can be summarized as follows:
“. . . the final state is limited by boundary conditions.”
“The boundary values are the conditions that constrain the climate over the long-term . . . ”
“. . . and that this state depends mostly on the boundary conditions.”
Our closing summary in the current post was specifically and purposefully stated within the framework of the mathematics and physical domains that were the subjects of the post. The summary also requested additional information about the BCs.
Here’s the Question Within the framework of GCMs and all other factors summarized above,
(1) identify the boundaries of the physical domain that are represented in GCMs, e.g define the surface B which constitutes the invariant boundary of the whole system under study.
(2) describe the Boundary Condition(s) (BCs) that are imposed on the boundary, and
(3) describe the equation(s) and dependent variable(s) to which each BC that applies at the boundary B, e.g prescribe explicitely N functions Gi(x,t) defined on B such as for all dynamical parameters Fi(x,t) defined on B we have Fi(x,t) = Gi(x,t) for all x included in B.
Suggest a mechanism allowing to obtain a unique solution of the dynamical equations depending only on the boundary conditions and justify the time scale T at which this mechanism would start to operate.
Physics and mathematics successfully function only so long as an established and universally accepted nomenclature is honored.
Tomas
Thank you for another stimulating discussion.
There are a few things that leave me cold. The planet is not in thermodynamic equilibrium – so that’s not worth any further consideration. What does matter for climate is the instantaneous difference in power flux in and out of the system. This is of course integrated along satellite tracks – or measured as incoming solar radiation with a simple geometric projection onto the Earth’s surface. The difference appears as more or less heat in the planetary system. It is a simple matter to convert ocean temp to energy content for instance. Heat drives the system at an exponentially varying rate towards a transient radiative equlibrium at TOA where power in equals power out.
These are just applications of fundamental physical principles to the planetary system in which PDE’s play no part at all. The latter seems more akin to the many worlds interpretation of probabilities in Schrödinger’s wave equation – it’s just math.
It is climate data at all scales that provides the basis for including climate in the broad class of deterministic chaotic systems. Chaos is not defined rigorously in physical systems but is recognized in a set of common behaviors.
Climate models are very different – it is just math. Imprecision in both initial and boundary conditions – the practical distinction in this context escapes me – result in many different plausible solution trajectories that are a priori unknowable. This was Lorenz’s quandary. It is known without much doubt as the experiment has been done many times.
Cheers
“Well the boundary condition is the value of u(Xb,Yb,Zb,t) (or of its derivatives but I won’t complicate) on the boundary which, as you remember, is the sphere surface .”
No, it isn’t. Or doesn’t need to be. Take the heat equation. Common boundary conditions might be:
1. T=0
2. ∂T/∂n=0 Insulating boundary (Neumann), n is direction normal to the surface
3. ∂T/∂n = -a*T Robin (radiative etc) condition
Each is adequate, and the Robin condition corresponds to some very common physics. There are of course more complicated conditions like Stefan, which is a moving boundary with phase change. It doesn’t make sense to talk of specifying the value of something in these later cases. They are just values of something.
And note that the Neumann condition isn’t saying that the derivative (grad) of T is zero. You can’t specify that – it would be too many equations. You can specify the normal component. Boundary conditions are both simpler and more complicated than is described here.
It often helps to think about what a boundary really is. Solve heat eqn in a box with walls of finite thickness made of material with high thermal resistance, so the flux is small. Flux is continuous across the inner boundary, so that implies a zero gradient in the medium where the thermal conductivity is not zero. Neumann condition. But you didn’t have to regard the inner surface as a boundary. You could solve the heat equation up to the outer boundary, taking account of the low conductivity of the wall material. Then you would need an outer bc, but it actually doesn’t matter what you apply there. The bc just becomes a shorthand for a region (wall) whose behaviour you can simplify.
“They are just values of something.”
That was a fragment of a longer thought that escaped prematurely. Please ignore.
Hurting a little I guess, possibly the “I am a mathematician comment” was a bit premature?
Nick Stokes | June 26, 2018 at 5:56 pm
–
“Well the boundary condition is the value of u(Xb,Yb,Zb,t) (or of its derivatives but I won’t complicate) on the boundary which, as you remember, is the sphere surface .”
“No, it isn’t. Or doesn’t need to be.”
–
Well which one is it then?
“Or doesn’t need to be.” actually implies [in English] Yes, it is but let’s ignore that. Perhaps we need a Venn diagram with in out and Schrodinger overlapping spheres.
If you get what I mean.
“Well which one is it then?”
The specification quoted is not the meaning of boundary condition. It is a special type of boundary condition, called Dirichlet. But there are many other possibilities.
The insistence on rigorous mathematical clarity of nomenclature and in conceptualization is certainly praiseworthy. Yet it should not obscure or presume upon the intrinsic nature of physical problems. The ex ante premise that
goes a bridge too far. While nonlinearity is a necessary condition for chaos, it is far from being a sufficient one.
As it turns out, there are certain spatial scales over which the time-variation of surface temperature about its local long-term mean is virtually homogeneous, as shown by the high cross-spectral coherence of stringently vetted station records in various diverse regions of the globe. Thus, aggregate averaging of such records produces time-series of anomalies that are regionally invariant. While the spatial variability may indeed appear chaotic over a fractal globe, within a properly circumscribed climatic region —-and almost certainly in the global average–the spatial component is effectively constant.
Care to pass on your wisdom?
Word salad is no substitute for real world data tested against a cogent hypothesis?
It isn’t a word salad. It sensibly explains that you don’t have chaos just because of nonlinearity. In fact, it would be useful if folk who speak of “variations in space are as chaotic ” could say what they mean.
Strange bedfellows united in gobbledegook.
“Lorenz was able to show that even for a simple set of nonlinear equations (1.1), the evolution of the solution could be changed by minute perturbations to the initial conditions, in other words, beyond a certain forecast lead time, there is no longer a single, deterministic solution…” http://rsta.royalsocietypublishing.org/content/369/1956/4751
Nonlinearity is what drives chaos in models. But it is the behavior of the nonunique solutions to the set of equations – or rather the numerical approximations thereof – that characterize the temporal chaos of models.
There are dozens of chaotic oscillators across time and space in the Earth system. These are ‘quasi standing waves’ in the spatio-temporal chaos of the system. They form, persist and then shift under whatever lorenzian trigger applies. Completely analogous to vortices in a swift flowing mountain stream – indeed the same simple rules of chaos apply across the planet and from moments to ages. Perturb the flow and the number and location of vortices will change.
e.g. https://stateoftheocean.osmc.noaa.gov/
We have for instance oscillating states that when viewed as nodes on a network synchronize after which climate – regional and global – shifts.
https://watertechbyrie.files.wordpress.com/2017/03/tsonis-1-e1527733514997.jpg
“We construct a network of observed climate indices in the period 1900–2000 and investigate their collective behavior. The results indicate that this network synchronized several times in this period. We find that in those cases where the synchronous state was followed by a steady increase in the coupling strength between the indices, the synchronous state was destroyed, after which a new climate state emerged. These shifts are associated with significant changes in global temperature trend and in ENSO variability. The latest such event is known as the great climate shift of the 1970s… This is the first time that this mechanism, which appears consistent with the theory of synchronized chaos, is discovered in a physical system of the size and complexity of the climate system.” https://agupubs.onlinelibrary.wiley.com/doi/10.1029/2007GL030288
The idea of an invariate climate at whatever scale is so removed from the physical reality of the planet that it seems eccentric to say the least – but it is just this sort of unfounded hyper abstraction that allows so wild a claim. Explain to us how climate is invariate. Where is the data? Where is the science?
“Nonlinearity is what drives chaos in models. “
No, it isn’t. In fact, chaos in models emulates chaos in real flows. But non-linearity isn’t the source. The basic definition of chaos is that you can start with two points arbitrarily close together, and after enough time, they will be far apart. So you can’t fully predict a state then, because small uncertainties make big differences.
But it isn’t nonlinearity that separates. That is a property of the linearised equation. The equation
y’=y
does a very good job of separating neighboring starting points. It doesn’t seem like chaos, because the whole space expands as the trajectories separate. What the non-linearity does is allow the solution manifolds to fold back on themselves so that the separation looks like chaos.
” dozens of chaotic oscillators across time and space”
I’m seeing this a lot. What does chaos in space actually mean?
http://www.pnas.org/content/pnas/104/21/8709/F1.large.jpg
“Generic behaviors for chaotic dynamical systems with dependent variables ξ(t) and η(t). (Left) Sensitive dependence. Small changes in initial or boundary conditions imply limited predictability with (Lyapunov) exponential growth in phase differences. (Right) Structural instability. Small changes in model formulation alter the long-time probability distribution function (PDF) (i.e., the attractor).”
Models are chaotic without a doubt – and chaos is characterized by shifts between attractors in the fractionally dimensioned state space.
e.g. https://www.ibiblio.org/e-notes/webgl/lorenz_model.html
In the high dimensional state space of the climate system these are seen as shifts and regimes in climate data – discovered as far back as 1950 in Nilometer data over more than a millennia.
Are you being deliberately obtuse? This is a chaotic oscillator, a quasi standing wave or a strange attractor in its 20-30 year negative mode – pick your term. There are dozens of globally coupled oscillations in the Earth system.
https://earthobservatory.nasa.gov/IOTD/view.php?id=8703
At last, someone has forcefully pointed out the 800 pound gorilla in the room: climateers have been arguing about the value of “equilibrium climate sensitivity” without first bothering to ask the question of whether it even exists. Hughes and Milanovic very elegantly point out that for a system that is never in equilibrium, there can be no such thing as an equilibrium sensitivity. I’ve been trying to get that point across for years, now. Kudos.
“there can be no such thing as an equilibrium sensitivity”
And yet, the abstract of our hostess’ very recent paper starts out:
“Energy budget estimates of equilibrium climate sensitivity (ECS)…”
There are two equilibriums under discussion. One doesn’t apply to the Earth system and so is irrelevant. One intended to compare opportunistic ensemble projections to energy balance calculations using the same input data. I dismiss both the latter as having negligible scientific value.
I have no great regard for ideas of lag due to thermal inertia given large ocean warming and cooling on an annual basis driven by orbital eccentricity. Lags have a greater range than even sensitivity.
https://watertechbyrie.files.wordpress.com/2018/05/ceres_ebaf-toa_ed4-0_incoming_solar_flux_march-2000tonovember-20171-e1530073907432.png
And the reality is that the energy budget of the planet is dynamic change being the norm and not a steady state where the inflow equals outflow. In hydrology a steady state is when “velocity, pressure and other properties of fluid flow can be functions of time (apart from being functions of space). If a flow is such that the properties at every point in the flow do not depend upon time, it is called a steady flow.” Like energy flux in the Earth system – it is true in real streams only transiently as flows change.
Of course ECS is an imaginary concept. Every informed person gets that the doubling of deep glacial CO₂ levels from 180 to 360 ppm cannot have the same effect on climate that doubling interglacial levels from 280 to 560 ppm. The climate initial states are completely different and the feedbacks that can be recruited are very different.
But as with many imaginary concepts (like imaginary numbers), it can be a very useful concept, as it is a way to measure the effect of CO₂ on climate. That’s why we all go along with it.
of course it exists, kinda by definition which how all system metrics work.
hi, Steven. I’m looking for the information summarized here.
Any assistance will be appreciated.
@Javier “But as with many imaginary concepts (like imaginary numbers), [ECS] can be a very useful concept, as it is a way to measure the effect of CO₂ on climate.”
It isn’t “an imaginary concept.” It’s an invalid concept. “Equilibrium sensitivity” is a concept derived from reality, but in situations where there is no equilibrium, it is inapplicable. That makes it worse than useless: it gives people the idea that they can determine a causal relationship by studying something that doesn’t even exist. (And “imaginary numbers” are not an imaginary concept. They are a valid, well-understood concept given an unfortunate name by Descartes before anyone understood them. Gauss later remarked “That this subject [imaginary numbers] has hitherto been surrounded by mysterious obscurity, is to be attributed largely to an ill adapted notation. If, for example, +1, -1, and the square root of -1 had been called direct, inverse and lateral units, instead of positive, negative and imaginary (or even impossible), such an obscurity would have been out of the question.”)
“That’s why we all go along with it.” No, we don’t all go along with it.
Here is my take. Equilibrium climate sensitivity has meaning in context of the ‘CO2 as climate control knob’ theory. It has little meaning in context of the more dynamical, chaotic view of climate that I described in my recent debate presentation.
But, isn’t it the case that the earth cools so slowly, say, headed back into a glacial that there is effectly a temperature at which we can say that the earth is neither warming nor cooling? (and any temperature state which departs from that effective equilibrium temperature would then be out of equilibrium?)
effectly should read effectively
@Dr Curry. I respectfully disagree specifically with the idea that ECS can be used in the context of CO2 as a climate control knob if by that you mean it can tell whether or not CO2 is such a knob. Let’s assume that the climate is Lorenz chaotic, and that the “equilibrium” point is an attractor. Due to the very large number of other drivers, each varying in time, some periodic, others not, the attractor point will move around in time. Separating out the contributions of each of these drivers (clouds, atmospheric chemistry, biological activity, astrophysical activity, solar activity, volcanic activity, greenhouse gases, etc) would, if it could be done at all, require much more data than we have over a much longer period of time.
If you’re watching an oscilloscope trace that displays a phase diagram of a large number of inputs, some periodic, some random, some chaotic, all on different time scales, and you input your own signal linearly, what are the odds that you will see the effect? Actually, that would be a very, very interesting experiment to perform…
My point is that if you ASSUME CO2 is a control knob, then ECS makes sense. If you don’t, then it is not really useful
The problem with the Lorenz attractor analogy is that Lorenz has a fixed parameter for the Rayleigh number, which plays the role of the forcing. If you increase that parameter, i.e. the forcing, you get a different attractor with more energy. That is what we are doing to the climate state. The energy of the system is increasing with the forcing. The weather attractor of the future has no overlap with the weather attractor of the past.
“If you don’t, then it is not really useful”
Well, yes, because ECS is the response to altered CO2.
affonzarelli,
But Earth doesn’t cool slowly into the next glacial period. Sure it may take ~80,000 years from now to next glacial maximum, but this occurs with many abrupt changes, both warming and cooling, along the way. The colder it gets the greater the abrupt changes.
Egads. My incompetence with quotations knows no bounds
Peter, that’s my point (i think)… At 80,000 years that works out to just .05C per millenium. So as the earth plods along at basically the same temperature any warm spells/ cool spells would pull the earth out of equilibrium. (at the very least warm spells?) Right now, we’re roughly .8C above that effective equilibrium as evidenced by, say, sea level rise and (i think) outgassing of co2. There is a temperature at which the earth would effectively not be warming/cooling. (that temperature would be your equilibrium state temperature)…
*i think the claim with co2 is that we’re pulling the temp so far out of equilibrium that we’re creating a new equilibrium temp.
“Albedo forcing at the LGM is estimated as c. -3.2 W/m2
CO2 forcing (no feedback) for a doubling is detonated as 3.7 W/m2
Your statement that ECS has little meaning is roughly equivalent to saying that albedo has no discernible effect on ice ages.”
This is erroneous because the ice ages were not a result of global energy imbalance, but rather of local energy changes, specifically at high Northern latitudes, and specifically during summer.
Such changes of clear Northern summer days were on the order of 60W/m^2:
https://i.stack.imgur.com/05ADi.png
The temptation of those conceiving of the world in terms only of CO2 is to simplify and imagine process were driven by similar global mean changes, but that is incorrect.
It is indeed erroneous. It is also not what I claimed. You will note that I did not say the ice age was a result of global energy imbalance, merely that the magnitude of albedo forcing at LGM is roughly equivalent to the non-feedback forcing from a CO2 doubling.
It’s a good job that I claimed no such thing then, is it not? Perhaps you can provide a link to anyone claiming such a thing, as you seem to think there are many of them?
What I did claim is that saying that CO2 is not a control knob on climate is “roughly equivalent” to saying that albedo changes have no effect on ice ages. The magnitude of total radiative forcing from albedo at the LGM is about the same as CO2 forcing at doubling, although of opposite sign. The route to getting to these forcing changes is, as you note, quite different.
Now, let’s see if I can get the quotations right for once.
The talk about forcing here is irrelevant to the point made by Michael. ECS is an idealized concept that is flawed and relies on a cartoon picture of the climate system.
I am very pleased to see this discussion of ECS.
I have always understood that accepting the undefined concept ECS is equivalent to handing the entire debate over to the alarmists.
Sure. That’s why it’s not the only metric used to characterise the system.
The point I’m trying to make is that the impact of co2 is clearly very large. As large as the albedo change at the LGM. That’s a good way to conceptualize why it’s been called a “control knob”.
“The magnitude of total radiative forcing from albedo at the LGM is about the same as CO2 forcing at doubling”
In waht way do you believe LGM radiative change is relevant to modern CO2 forcing?
I am easily amused obviously – this time with the wanky deliberations on the divergence theorem. As stated in the post the application of divergence theorem leads merely to energy conservation. Call me old fashioned but I would have started with the 1st law. In space all energy flux is electromagnetic and thus there is a convenient place to account for energy flux. There is no absolute requirement that energy in equals energy out and the difference represents dynamic warming and cooling of the planet. Equilibrium be damned.
https://www.facebook.com/Australian.Iriai/posts/1712078145575107
Changes in energy flux at toa are not merely due to greenhouse gases but there is large variability in outgoing energy due to deterministic chaotic shifts in Earth fluid dynamics. The evidence is incontrovertible. The alternative is
conveniently science and data free.
This contributes to ocean heat changes over many scales in time and space. The usual argument is that natural variation is random and thus sums to zero. Whatever the time frame under consideration. It isn’t and it doesn’t – believe it or not.
Robert
There are a few things that leave me cold. The planet is not in thermodynamic equilibrium – so that’s not worth any further consideration. What does matter for climate is the instantaneous difference in power flux in and out of the system.
Robert I cannot but agree with this statement . The devil is in the words “does matter” because this statement is only a half of the story .
Of course that the total energy variation (which is related to fluxes via Gauss’ theorem) matters . But it is not the only thing that matters .
Momentum conservation matters too . Navier Stokes is after all a way to say that momentum is conserved .
Mass continuity matters enormously .
Critical processes like phase changes and biological processes matter too .
Now all of this is expressed by PDEs . You want mass continuity ? You better check that you have a divergence free field . Otherwise if you think that you found a solution but it is not divergence free then you are in a very bad spot .
And it is precisely because you are interested in the energy flux OUT that you must know the dynamics of the system because it is these dynamics which will dicate the flux out and it cannot be deduced from the value of energy IN alone .
This is where the dynamical equations, boundary and initial conditions enter the game and these are PDEs . This is fundamentallly why we have written this post – to remind that physics without sound mathematics and rigorous definitions would be just a random collection of mysterious empirical rules and would reduce to a kind of religion .
I know that you know it too because you know that the very fact that chaos exists is due to the mathematical properties of the dynamical equations . ODEs for the temporal chaos (f.ex Lorenz) and PDEs for the spatio-temporal chaos :)
“You want mass continuity ? You better check that you have a divergence free field .”
Not true. The mass continuity equation is
https://s3-us-west-1.amazonaws.com/www.moyhu.org/2018/06/consmass.png
Divergence (of ρu) tells you how fast the density is changing.
Tomas
I am wary of mistaking the map for the territory – especially when the map is so fragmentary and there is no convenient X to mark the spot. It is all a fluid flow problem of course – your mountain stream and the entire planet – that as a hydrodynamicist I have some familiarity with.
“You can see spatio-temporal chaos if you look at a fast mountain river. There will be vortexes of different sizes at different places at different times. But if you observe patiently, you will notice that there are places where there almost always are vortexes and they almost always have similar sizes – these are the quasi standing waves of the spatio-temporal chaos governing the river. If you perturb the flow, many quasi standing waves may disappear. Or very few. It depends.”
https://watertechbyrie.files.wordpress.com/2017/08/river-in-mountains.jpg
There are great, coupled turbulent cyclones and anticyclones across the planet driving ocean gyres, upwelling patterns, heat transport and shifts in ice, cloud, biology and dust that modulate the global energy budget over moments to ages – according to that very fine Greek hydrologist Demetris Koutsoyiannis.
And that we can see – at least in the atmosphere – as easily now as your mountain stream.
https://earth.nullschool.net/#current/wind/surface/level/equirectangular
We know the nature of changes in the system from climate data at many scales. The system is dynamically chaotic – there is regime change and persistence. We have satellite data from last century that is suggestive and much better data from this century that is compelling. There are large changes in the global energy dynamic with shifts in ocean and atmospheric circulation. We have millennial scale related hydrological data that shows perpetual, chaotic change in the climate system.
But I doubt that we have the tools to calculate a unique, deterministic trajectory of a climate future. ‘Perhaps we can visualize the day when all of the relevant physical principles will be perfectly known. It may then still not be possible to express these principles as mathematical equations which can be solved by digital computers. We may believe, for example, that the motion of the unsaturated portion of the atmosphere is governed by the Navier–Stokes equations, but to use these equations properly we should have to describe each turbulent eddy—a task far beyond the capacity of the largest computer.’ Lorenz 1969 – and no – we are still not there.
There are people of course who can never understand – they are thus denied the beauty of vistas beyond this threshold idea. But such is life.
Cheers
As far as I remember this is a significant improvement on the previous post.
And for me helpful.
When no specifiable probability destribution of the solutions of GCMs) or the problems they purport to approximate) can be expected what tells us this about ensemble methods?
“Nonlinearity is what drives chaos in models. “
Nick says
No, it isn’t. In fact, chaos in models emulates chaos in real flows. But non-linearity isn’t the source. The basic definition of chaos is that you can start with two points arbitrarily close together, and after enough time, they will be far apart. So you can’t fully predict a state then, because small uncertainties make big differences.
Please Nick you would do service to everybody and especially to yourself if you stopped writing about non linear dynamics (aka chaos) .
It is embarassing to see that you have really little to no idea about how and why chaos works . I could understand that you ask questions because you want to learn something but I can’t understand how somebody can write affirmative statements which are obviously wrong .
Non linearity is a necessary but not sufficient condition for chaotic behaviour . This is a proven theorem so you better accept it .
Necessary conditions are what drives systems so you better accept it too .
But as they are not sufficient, one has to look for other conditions .
This is the reason why there is not ONE road to chaotic behaviour but many .
Intermittency, crises, chaotic transients and homoclinic orbits, stable and unstable manifolds etc are all different roads to chaos .
There actually is one accepted definition for what is a chaotic system (valid only for temporally chaotic systems) so I may as well give it to you :
A chaotic system is a system which has at least one positive average Lyapounov coefficient .
Of course this correct definition is not what you wrote .
Once this definition given, one can prove several theorems . One of them is the exponential divergence of orbits often called improperly “sensibility to initial conditions” .
So this dynamical behaviour is one of many consequences of the definition but not the definition itself .
After that you can start to look for systems with positive Lyapounov coefficients and try to understand why it is so and what that means and arrived at that stage you start to learn non linear dynamics .
Important caveat which I gave many times but that I am not sure that it talks to everybody is that all of the above deals with temporal chaos only (e.g with non linear ODEs with only 1 variable t) . Climate is spatio-temporal chaos (e.g non linear PDEs with spatial and temporal variables) .
While the temporal chaos is relatively well understood, spatio-temporal isn’t so that insights from the former do not transport to the latter .
I have specifically mentionned in the original post the case of the ergodic theorem which is fundamental to study the notion of probabilities of states in the phase space .
Divergence (of ρu) tells you how fast the density is changing.
Yes you do not need to copy what we already said in the first post when speaking about continuity equations .
And ?
And it is wrong to say the solution must be divergence free.
Really ? :)
Tomas,
I understand very well how chaos works and the role of nonlinearity. I wrote my PhD thesis on the matrix Riccati equation.
“Of course this correct definition is not what you wrote .”
It is entirely consistent with what I wrote. Your statement is equivalent to saying the linearised coefficient matrix has a positive eigenvalue. That is where the spreading of solutions comes from. And y’=y is such an equation.
“While the temporal chaos is relatively well understood, spatio-temporal isn’t”
Indeed it isn’t. I’m still waiting for a definition.
It sensibly explains that you don’t have chaos just because of nonlinearity. In fact, it would be useful if folk who speak of “variations in space are as chaotic ” could say what they mean.
While it is not sensible to focus on non linearity when talking about chaos because it is only a necessary condition as I explained above, it is sensible to try to understand spatio-temporal chaos .
I will explain what we mean and try to be as simple as possible . I need to assume that the notions of infinite dimensional Hilbert spaces are known . If not, do not read farther it will be a waste of time .
1) Spatio-temporal chaos theory deals with functions depending on space and time and exhibiting spatial pattern formations . Very simplified I could say that spatio-temporal chaos theory is a spatial pattern theory .
2) The first stage is classical, we write the dynamical equations governing the system which are PDE . I take as example a chaotic reaction-diffusion system where the PDE are known .
We then supppose that the solution for given initial conditions is of the form :
u(t,r) = Sum over k of Ak(t).Uk(r) .
For every k, Uk is the corresponding spatial pattern . Ak is the spatial mode k amplitude .
3) We can take now a step where we assume that the k spatial mode functions are orthogonal (this can of course be wrong but we assume that it is true for the example) . The solution u(x,t) lives then in an infinite dimensional phase space of functions where we found an set of orthogonal functions . This is fundamentally different from the temporal chaos where the phase space is finite and generally low dimensional .
4) Using then orthogonality we obtain ODes which permit to find the spatial mode amplitudes . As these are functions of time, we can use the temporal chaos theory and especially look for positive Lyapounov coefficients . If there are none, the system is not chaotic and the spatial patterns are either stable or periodic depending on boundary conditions . However if there are several we will see emerging spatial patterns which will continuously change . The “chaotic variation in space” is then precisely the “chaotic variation of the spatial modes (patterns)” .
An example of spatial modes in climate are oceanic oscillations . We clearly see that ENSO is the most critical spatial mode of the system but as we don’t know all the other modes nor the spatial mode amplitudes, nor the dimensionality and orthogonality of the modes , the predictability of this particular mode as well as of all other modes is poor .
A caveat . I simplified so much that I don’t want that emerges an impression that the above model is valid for all times and even less for all spatio-temporally chaotic systems .
In reality this model doesnt allow to say what happens a long time after the critical spatial modes started to grow . We suppose that we started with an initially homogenous system (e.g no pattern) and our analysis showing the pattern dynamics is valid only when we are very close to the initial state . What happens later is that the modes start to interact, unstable states appear and disappear, we can no more suppose orthogonality thus entering terra incognita .
Current browser statistics for word frequencies in this thread:
Energy 203
Temperature 61
Chaos 54
Entropy 5
Dissipation 2
Free Energy 0
Maslow’s Hammer strikes again?
I understand very well how chaos works and the role of nonlinearity. I wrote my PhD thesis on the matrix Riccati equation.
“Of course this correct definition is not what you wrote .”
It is entirely consistent with what I wrote. Your statement is equivalent to saying the linearised coefficient matrix has a positive eigenvalue. That is where the spreading of solutions comes from. And y’=y is such an equation.
Sorry Nick but you obvously speak about things that you have not studied (being polite here) and the discussion would be more efficient if you stopped this because we wouldn’t waste time dealing wrong, approximate or irrelevant statements . Asking question is of course OK but throwing in irrelevant , wrong or unproven statements as truths is not .
All what you said above is at best irrelevant again .
Riccati equation is interesting in control theory but you won’t see it mentionned even once in any textbook about non linear dynamics because it has nothing to do with chaos .
So you wrote a paper on linearization of some non linear ODE ?
I congratulate but it is of no value in this thread . This doesn’t mean that it is not interesting but you wrote it so long ago that it could not have had any relation with chaos theory which didn’t exist yet (the term has been introduced by Li, Yorke and Rössler only in 1975) and it was recognized as a specific field of physics even later .
I don’t know why you speak about linearized coefficients .
I have already noticed that you have a bad habit to reduce everything to some linearity but it really doesn’t work for chaos where you can’t linearize (almost) anything .
y’+y = 0 is just some random linear ODE, what has that to do with anything and especially with chaos or our post ?
The important concepts for non linear dynamics are invariants sets , topology in the neighbourhood of fixed points , characteristic values, convexity etc but there is really little that can be understood with linear considérations and approximations .
Robert
But I doubt that we have the tools to calculate a unique, deterministic trajectory of a climate future. ‘Perhaps we can visualize the day when all of the relevant physical principles will be perfectly known. It may then still not be possible to express these principles as mathematical equations which can be solved by digital computers. We may believe, for example, that the motion of the unsaturated portion of the atmosphere is governed by the Navier–Stokes equations, but to use these equations properly we should have to describe each turbulent eddy—a task far beyond the capacity of the largest computer.’ Lorenz 1969 – and no – we are still not there.
Well personally I have no doubts . Not only we have not the Tools but even if we had them the task is impossible .
If we had the tools we could perhaps prove unicity . Technically one “just” needs to find correct bounds for the solution or for some functionnal and it’s done .
It is not so easy because it could not be done yet for N-S in the general case .
By Tools here I mean equations .
But solving them really is completely another matter and it is this impossibility what I have no doubts about .
So if we think rationally and agree on the impossibility to find the unique solution if it exists what is left ?
Personally I think that only a probabilistic approach is possible .
That’s why went quite deep in the ergodic theory – it makes the connection between trivial every day simple averages and the attractor where all orbits live .
Now this works for temporal chaos (not always but often) but there is nothing for spatio temporal chaos .
The graal is then to find an equation (totally analogous to the Schrödinger equation in MQ) where the unknown function is a probability distribution density in the phase space (OK it’s infinite dimensional but that can be dealt with) and no more the dynamical variablesthat we have been torturing during these past 30 years .
To my knowledge there is sofar little progress in this direction and , of course , the numerical “ensemble averages” are probably more a regression than a progress .
Tomas Milanovic: To my knowledge there is sofar little progress in this direction and , of course , the numerical “ensemble averages” are probably more a regression than a progress .
Thank you again for your many comments.
Excellent comments. We need to get out of our own way first. Starting with some institutional introspection.
One more comment on the Navier-Stokes equations (NSE), for the benefit of those who believe that climate models must be right because “they are based on physics,” Implied in the definition of “physics” is the notion that the equations in our models accurately describe relationships among measurable physical quantities based solely on the first principles of the laws of physics.
The NSE are simply mathematical statements of the conservation of mass, momentum, and energy. Nothing controversial there – until one asks “mass, momentum, and energy of what?” Well, of a “continuum”, which is an amorphous, voidless blob in which (for Newtonian fluids) stress at every point is proportional to strain (i.e. deformation) rate at that point. The NSE definitely describe the relationships among various quantities in space over time, albeit in a substance that doesn’t exist in reality. I don’t want to get into a debate about the continuum approximation, but I do want to note that the NSE do break with physics at that level, and the effect of the “crack size” is unknown.
One thing the NSE do not have in them is any evidence of the ability to predict turbulence, either its onset or structure. In fact, direct simulation places requires such fine mesh and tiny timesteps that no computer could calculate the transition from laminar to turbulent flow of water in a tiny tube (even if the NSE inherently could do so, something no one knows). For practical problems, larger scale meshes and longer timesteps are required. To make this possible, Reynolds averaging is used. Basically, the components of velocity at every point are broken into the sum of a steady velocity and a fluctuating component. When viscosity is introduced, an unfortunate thing happens. The number of variables becomes larger than the number of equations. Suddenly, the break with “physics” is complete, since the equations are underdetermined. They cannot accurately predict anything because they have either no solution, or an infinite number of solutions.
Attempts to overcome this by adding physically valid equations as constraints never works, because the number of variables keeps growing faster than the growth in number of equations. The work-around is to employ equations that don’t add more variables, and use their adjustable parameters to control the fidelity of the model compared to, say, wind-tunnel measurements. These adjustable parameters and their equations have no physical meaning. An immediate corollary is that they also have no universal or even predictable value. Any CFD work involving turbulence and Reynolds averaged Navier Stokes is basically an exercise in curve-fitting. One takes a guess at the parameter values, makes a few flow predictions, then performs measurements on a physical model in a real flow. The parameters are adjusted and measurements repeated until the CFD model is acceptably close to the physical model in a real flow. Any significant change to the physical model or the real flow conditions will require a repeat, because the adjustable parameters have no universality.
So don’t hang your hat on the idea that the Navier Stokes equations as used in CFD are ironclad expressions of laws of physics as solid as conservation of mass, momentum, and energy. They retain some of the solid nature of those laws, but are removed from first principles by an unknown (and probably unknowable) amount by the introduction of non-physical equations and parameters.
Excellent comment Michael. I would just add that in some areas of application such as aeronautics, there is a vast history of testing and model development and indeed tuning. So there is a range of flows where we are rather confident. This includes flows with mild pressure gradients and no significant flow separation or convection. But that’s a quite small part of the range we would need to predict to certify an aircraft for example.
The other thing to stress is that engineering applications of the NSE’s are highly idealized. So things like onset flow turbulence are assumed to be very small. Clouds, precipitation, and basically all energy transfer mechanisms other than inertial mechanisms are usually small.
By what mechanisms an open system that is clearly operating far from equilibrium will attain such an equilibrium state has never been defined.
Lorenz answered this in DNF 1963:
Never.
Will this continue to be an insuperable intellectual barrier to the modelling-driven climate science community?
Michael
I don’t want to get into a debate about the continuum approximation, but I do want to note that the NSE do break with physics at that level, and the effect of the “crack size” is unknown.
Well actually this has been studied . I have read that paper a long time ago and will try to find where it is even if this task will be very difficult .
So the following is from memory .
They did experiments on Rayleigh-Taylor instability which leads to spatio temporal chaos ( https://en.wikipedia.org/wiki/Rayleigh–Taylor_instability ) .
The originality of the paper is that they wanted to precisely find out when and how the behaviour will start to diverge from Navier Stokes equations because of what you said – a fluid is not a continuum ..
For that they solved the fluid behaviour by only using the dynamical equations on the molecular level (so without N-S) .
Obviously this method is limited to a small number of molécules (I Believe a few hundreds) what is very small indeed .
What they found out was that the divergence starts to happen only at very small scales .
Above these scales (I don’t remember exactly the size) there were no measurable differences between dynamics computed by N-S and dynamics computed by molecular interactions which Don’t postulate continuity .
The conclusion was then that the N-S was a very good approximation of the molecular level equations above a certain size . In usual applications we are far above these sizes so that the use of N-S is legitimate .
Of course numerical methods to solve N-S have many other and more severe problems that we mentionned ut they are not related to the non continuity of fluids at molecular level .
Tomas
Thanks for the information, and I look forward to the paper (if you can find it; if not, no worries). I wasn’t aware of a direct simulation approach like that.
Actually, connecting continuum mechanics to molecular dynamics has been done theoretically in that the Navier-Stokes equations have been derived from the Boltzmann equation (of kinetic theory of pure gas fame). However, it is a matter of taking a limit, which wipes out some of the features of molecular dynamics and, in my view, removes the mechanism by which turbulence might be predicted. (Here’s a link to just one such paper: http://www.dartmouth.edu/~cushman/papers/2018-Boltzmann-to-NS.pdf) And the closure problem still remains for any practical application.
Dr. James Kliegel spent the last years of his life working on a derivation of equations of fluid dynamics based on the Boltzmann equation, but with a unique twist. He discovered that Boltzmann had thought that temperature might not be an isotropic property, but that assuming that it was would have little effect on his results. Kliegel changed that assumption, and was able to produce a closed set of Maxwell moment equations of the Boltzmann equation, and it was evident that this set would be capable of predicting the onset and structure of turbulence with no non-physical “turbulence models.” He actually patented it (https://patents.google.com/patent/US7209873B1/en). I helped him try to sell someone on implementing it in code, but everyone we talked to either didn’t understand it, or was too heavily invested in his own methodology. It would be interesting to pursue this line further.
The problem with the Lorenz attractor analogy is that Lorenz has a fixed parameter for the Rayleigh number, which plays the role of the forcing.
No the problem with Lorenz attractor analogy (which could have been known by everybody who read the first post) is that there is no analogy .
Lorenz equations are an example of low dimensionnal (generally 3) temporal chaos . Climate is an infinite dimensional spatio-temporal chaos .
Making analogies between concepts when there are none only leads to increase the confusion .
you increase that parameter, i.e. the forcing, you get a different attractor with more energy. That is what we are doing to the climate state.
And this is the kind of confusion that comes when one does not know what one is doing and uses wrong analogies . There are 3 parameters in the Lorenz system . Changing any of the 3 changes the dynamics . For some there is even no chaotic regime . This has absolutely nothing to do with “energy” alone . This has to do with the nature of the dynamical equations which can change an attractor even if the energy doesn’t change .
Nothing analogous can be “done” to the climate because the phase space is infinite dimensional and there is an infinity of “parameters” . The “parameters” are btw no constant numbers but functions .
The energy of the system is increasing with the forcing. The weather attractor of the future has no overlap with the weather attractor of the past.
God ! The energy increases trivially if the flux is negative (Gauss theorem) . This is true regardless whether the system is chaotic or not and it has still less to do with any “attractor” if it exists .
The second sentence is not even wrong .
How do you imagine “the weather attractor” ? How many dimensions ? What topology ?
Besides, and this is a definition, an attractor is an invariant set !
So what can it possibly mean that an invariant set in the past “has no overlap” with the same invariant set in the future ?
If you say that it means that it is not invariant and therefore not an attractor, you win .
I suppose that you confuse an attractor which is an invariant set of points of the phase space which contains all points of the dynamical orbits with a point of the dynamical orbit moving inside the attractor .
All this confusion can and will happen when one uses the temporal Lorenz chaos and extrapolates it to the climate .
I strongly advice that if the subject is climate/weather or more generally spatio-temporal chaos, do not speak about Lorenz unless you know very well what you are doing .
But if the latter, you’d probably not do it anyway :)
Tomas, the forcing is an invariant for a weather-like attractor, but is not an invariant for a changing climate. When you change the forcing, as with the parameter in the Lorenz attractor, you change the system and the attractor itself. Basically you have more energy in the system leading to a different set of possible states. The Lorenz attractor can be used to illustrate this by changing its normally held-constant forcing parameter. The current and future warmer climates have increased amounts of energy so it stands to reason they have a different attractor in phase space that does not overlap with a cooler climate. Changing the forcing parameter gradually in the Lorenz system makes it non-ergodic. This is like climate change.
I would like to make a general comment .
The reason that motivated my contribution to this post was that I was genuinely interested in what kind of mathematics (if any) is happening in the heads of the proponents of catastrophical global warming, CO2 über alles and climate is a boundary value problem .
By now I have read all the posts in this thread and I observe that not a single one of these proponents was able to answer the relatively simple questions we asked at the end of the post .
There was some confused irrelevant talk about “imbalances” , “forcings” and “equilibriums” yet still no answer .
Perhaps somebody will come with something that makes sense but sofar it seems that they are really unable to mathematically justify any of the slogans .
“I observe that not a single one of these proponents was able to answer the relatively simple questions we asked at the end of the post”
The questions are answered in the general documentation of the models. CAM 3 is a good example, although it is atmosphere only. The terrain coordinate system is described in 3.1.1, including a complete top and bottom condition (3.1 and 3.2).
The notion of boundary conditions that you supply is very limited, as I noted above. The proper understanding is of relations determining stress and fluxes. This is set out in section 4.10.1 for land, and 4.10.2 for ocean.
3.1.5 Energy conservation
We shall impose a requirement on the vertical finite differences of the model that they conserve the global integral of total energy in the absence of sources and sinks. We need to derive equations for kinetic and internal energy in order to impose this constraint. The momentum equations (more painfully, the vorticity and divergence equations) without the $ F_U, F_V, F_{\zeta_H}$ and $ F_{\delta_H}$ contributions, can be combined with the continuity equation
$\displaystyle \frac{\partial}{\partial t} \left( \frac{\partial p}{\partial\eta… …ial}{\partial \eta} \left( \frac{\partial p}{\partial\eta} \dot\eta \right) = 0$ (3.59)
to give an equation for the rate of change of kinetic energy:
$\displaystyle \frac{\partial}{\partial t} \left( \frac{\partial p}{\partial\eta} E \right)$ $\displaystyle =$ $\displaystyle -\nabla\cdot \left( \frac{\partial p}{\partial\eta} E {\boldsymbo… …rtial}{\partial \eta} \left( \frac{\partial p}{\partial\eta} E \dot\eta \right)$
$\displaystyle \phantom{=}$ $\displaystyle – \frac{R{T_v}}{p} \frac{\partial p}{\partial\eta} {\boldsymbol {… …bla p – \frac{\partial p}{\partial\eta} {\boldsymbol {V}}\cdot\nabla\Phi – .$ (3.60)
The first two terms on the right-hand side of (3.60) are transport terms. The horizontal integral of the first (horizontal) transport term should be zero, and it is relatively straightforward to construct horizontal finite difference schemes that ensure this. For spectral models, the integral of the horizontal transport term will not vanish in general, but we shall ignore this problem.
This is just a cursory glance at their discussion. They are going to ignore the problem. Not going to try to figure out how much error it introduces, just simply ignore it. Interesting.
“They are going to ignore the problem. Not going to try to figure out how much error it introduces, just simply ignore it.”
So what do you think are the consequences of ignoring it?
They didn’t say they were not going to try to figure it out. There is actually a two-stage process for trying to monitor deviations from energy conservation. One is this relation; the other is the “energy fixer”, sec 3.1.20, which monitors energy conservation.
I gave the link to CAM 3 documentation, because it is all nicely hyperlinked. They are actually up to CAM 5, and the corresponding doc in PDF is here. It handles this part quite differently, as described in sec 3.1.6.
Well the difference is that I defined all possible boundary conditions with a single line e.g u(Rb,t) (or combinations of its derivatives) =g(Rb,t) where Rb is a point on the boundary and g is an arbitrary function defined on the boundary . This is the proper understanding of boundary conditions and it applies not only to the climate – it applies to any PDE .
On the other hand you wrote a page giving only a non exhaustive list of random examples which were all covered by our definition anyway . Besides you obviously missed many because a list of examples is not how one does mathematics .
If I didn’t comment it was because your page was useless,, had no added value and one can only wonder why you cluttered the thread with something that has been already said better and with space economy in the first post .
We are also obviously not interested by what is in some documentation of some random numerical software . The question is asked for the whole system and it doesn’t depend on any software . It depends only on the physics or proposed physics that governs the whole system . Clearly the atmosphere alone is not the system unless you tell us that for you it is .
“We are also obviously not interested by what is in some documentation of some random numerical software . The question is asked for the whole system and it doesn’t depend on any software “
No, your question, featured in the post, asked:
“identify the boundaries of the physical domain that are represented in GCMs”
And I showed what an actual GCM said. It is not random numerical software, but is a widely used and representative GCM. Lack of interest in how GCM’s actually do things, including the boundary conditions they actually use, is a major failing of this post. The rigor and analysis of the CAM 3 document is far superior to what is offered here.
From the perspective of energy balance models (EBMs), the answers are very simple. Note that these are based on the energy budget terms.
– The boundary condition is the net radiative forcing at the top of atmosphere. This is an energy flux usually expressed in W/m2 averaged over the surface area of the sphere. An imbalance at this boundary implies by Gauss’s Theorem a gain of energy in the interior volume (dH/dt), and that shows up as an increase in heat content. Even a 1 W/m2 imbalance maintained over decades is easy to measure in the ocean heat content gain which is the main reservoir. This balance is done in EBMs. The imbalance or heat content gain currently is estimated at 0.7 W/m2.
– As the net radiative forcing changes (e.g. by adding GHGs or changing the net solar input) there is a response and an imbalance. The equation is
dF=dH/dt+dR
where in EBMs, dR (the response) is taken as a linear function of the surface temperature, lambda*dT.
lambda itself is dependent on the GHGs in the atmosphere and governs the sensitivity in the limit when the imbalance (dH/dt) goes to zero, as in equilibrium.
Tomas needs to familiarize himself with EBMs because they do use Gauss’s Theorem with the forcing change and the resulting imbalance in the budget to deduce what the equilibrium state would be after the transient imbalance is removed.
– EBMs present it as a purely boundary problem whereby a forcing change leads to a temperature change irrespective of details of the initial state.
Above, there is a tangent regarding the last glacial max.
I thought the forcing arguments were irrelevant, but perhaps this is a pertinent case of global radiative forcing versus dynamical fluctuation.
As vtg raises, the global mean radiative forcing of the LGM was negative with respect to present day, indicating global cooling in the RF centric view.
But, the proxy measurements of the LGM indicate warmer than present temperatures over much of the tropics:
https://upload.wikimedia.org/wikipedia/commons/thumb/1/19/CLIMAP.jpg/300px-CLIMAP.jpg
During modern winter, subtropical subsidence high pressure areas are larger and more intense than they are during summer ( in a given hemisphere ). This is reasonable given the polar cooling and steeper than in summer gradient of potential temperature. An analog is that during the LGM, more intense subtropical subsidence zones led to reduced albedo and increased temperature relative to present day.
In this way, global radiative forcing was reversed and even overwhelmed by dynamic changes to circulation for large portions of the earth in the most basic measure – temperature.
That map is based on data published in 1981.
Yes, evidently the process of ocean core drilling is very expensive and this hasn’t been repeated a la CLIMAP. But, there was MARGO (Multiproxy Approach for the Reconstruction of the Glacial Ocean surface).
I have changed the palette of the original MARGO LGM winter SSTs image to better see the warming areas in pink:
https://i1.wp.com/turbulenteddies.files.wordpress.com/2018/06/margo.png
CLIMAP and MARGO are fairly consistent, though they may differ in objective analysis and MARGO indicates a lot of area as unknown.
So these warming areas from dynamic change may well be a good example.
It is important to note that something can be chaotic at a great range of scales, from controlling to trivial. A dropped rock falling through the air may wiggle chaotically just a little, due to the turbulence in the air flow around it, but it does not significantly affect where it lands. A dropped feather in the turbulent wind may blow upward and far away before finally landing, who knows where.
Thus saying that climate is somehow chaotic, without specifying the nature and relative scale of this chaos, says nothing scientific as far as what climate does or will do. The climate models often exhibit chaos, but it is at a scale too small to matter as far as long run predictions are concerned.
In short, whether or not climate is chaotic in any important sense has yet to be determined. Simply saying that climate is chaotic, while perhaps no doubt true, does not change this deep uncertainty. In fact it is a grand challenge to say how chaotic climate is, a challenge that does not seem much pursued.
I am a bit puzzled by this talk of temporal versus spatio-temporal chaos. What bothers me is that chaos is a mathematical property and as such it is neither temporal, spatial or spatio-temporal. Chaos is a property of certain equations, or sets of equations, and these are not in themselves about anything, much less about things in space and time.
Take the logistic equation, for a simple example. It could be used to describe change over time, hence temporal. Or it might describe change over a line, hence spatial. Or change of something in space, over time, hence spatial and temporal (but perhaps not spatio-temporal).
I therefore assume that, in the present context, temporal and spatio-temporal chaos refer to specific applications of chaos theory to certain physical systems. So far as I can tell these specific cases have not been explained. Perhaps I just missed it.
My conjecture, which may well be false, is this. Temporal chaos refers to the behavior of total states, of the system in question, over time. The trajectories in the state space, where each point is a total state, especially when they are in a strange attractor. This is what normal discussions of chaos often are about.
Spatio-temporal chaos then refers to how things change over time within the successive states. The spatial variability of the temporal chaos, if you like. These variations can be very complex and they are not simply bound by the attractor. (Although if the total state is bounded that might bound individual features of the state as well. The wind can only blow so hard.)
Is this close to correct? Or is spatio-temporal chaos something else entirely?
Chaos is a property of certain equations, or sets of equations, and these are not in themselves about anything, much less about things in space and time.
Is one if the very many examples here of mistaking the map for the territory. It is something that goes well beyond logical fallacy to scientific delusion. There is all sorts of talk about esoteric math and physical principles that are fundamentally misguided – because the map from first principles is misleading. If there are governing equations for climate – we don’t know what they are. It is not a priori predictable and that is the point – it may be insoluble using any existing mathematical tool – and only data enables us to see the simple rules at the heart of chaos. Chaos is defined as chaos if systems behave in accordance with the rules.
e.g. http://mathworld.wolfram.com/Chaos.html
A brand new math is required – the network and node approach of Marcia Wyatt’s stadium wave or Anastasios Tsonis’ synchronized chaos show initial promise as proof of concept. I have no doubt that many other tools will emerge over time for this intractable problem. My inclination is to agree with Georg Sugihara and throw away the math entirely.
“Trying to manage a major fishery with such a primitive understanding of its biology seems like folly to George Sugihara, an ecologist at the Scripps Institution of Oceanography in San Diego. But he and his colleagues now think they have solved the mystery of the Fraser River salmon. Their crucial insight? Throw out the equations.”
http://www.pnas.org/content/112/13/E1569.full
Deterministic chaos is a property of complex and dynamic systems. A falling rock is far from complex – the turbulence of wind bearing a feather is. A simple set of nonlinear equations evolve in time – temporal chaos – other system evolve in time and space – spatio-temporal chaos. Chaos in this broad class – climate, models, economics, biology, avalanches, etc. – of dynamically complex systems has a similar origin. Decades ago in Quaternary Science climate was described – I don’t remember by whom – as tremendous energies cascading through powerful subsystems. It is the interactions of of these subsystems that result in the dynamic response of systems to small perturbations. Control variables push systems past a threshold and the systems then fluctuate wildly before settling into a new state with different means and variance.
https://watertechbyrie.files.wordpress.com/2014/06/bifurcations1.png
“Climate is ultimately complex. Complexity begs for reductionism. With reductionism, a puzzle is studied by way of its pieces. While this approach illuminates the climate system’s components, climate’s full picture remains elusive. Understanding the pieces does not ensure understanding the collection of pieces.” Marcia Wyat
At phase shifts there are interesting properties. “We develop the concept of “dragon-kings” corresponding to meaningful outliers, which are found to coexist with power laws in the distributions of event sizes under a broad range of conditions in a large variety of systems. These dragon-kings reveal the existence of mechanisms of self-organization that are not apparent otherwise from the distribution of their smaller siblings. We present a generic phase diagram to explain the generation of dragon-kings and document their presence in six different examples (distribution of city sizes, distribution of acoustic emissions associated with material failure, distribution of velocity increments in hydrodynamic turbulence, distribution of financial drawdowns, distribution of the energies of epileptic seizures in humans and in model animals, distribution of the earthquake energies). We emphasize the importance of understanding dragon-kings as being often associated with a neighborhood of what can be called equivalently a phase transition, a bifurcation, a catastrophe (in the sense of Rene Thom), or a tipping point. The presence of a phase transition is crucial to learn how to diagnose in advance the symptoms associated with a coming dragon-king. Several examples of predictions using the derived log-periodic power law method are discussed, including material failure predictions and the forecasts of the end of financial bubbles.” https://arxiv.org/abs/0907.4290
Dragon-kings demonstrate the futility of cramming chaos into a conceptual framework ill suited for the purpose. Abandon preconception if you would cross this portal. Me – I am going to the beach to write poetry or play bongos to the freetime music of wind, waves, flocks of birds wheeling overhead and the laughter of children.
“Chaos is a property of certain equations, or sets of equations, and these are not in themselves about anything, much less about things in space and time.”
A quote of course…
Not sure what you are asking for, Robert, as I am not citing someone else. This is my field. Physics often finds, or tries to find, cases where specific equations apply. The logistic equation, for example, is widely used in science. But the abstract equation is not about anything physical. It is just math.
That was one of the points – it is far from just math.
Robert, you say “Is one if the very many examples here of mistaking the map for the territory. It is something that goes well beyond logical fallacy to scientific delusion.”
An equation is not a map. Maps are of specific things, but equations per se are not. The equation “x = 2y – 3z” is not about anything in particular. Of course equations are often used to describe physical situations, just as maps are. That is applied math and it can work to varying degrees of accuracy. But the fundamental properties of chaos are mathematical properties. They are not about or based on any particular physical situation.
This is why chaos was discovered by a mathematician, Poincare, not a physicist. What Lorenz did was discover an important case of chaos (50 years later), but this was because he knew of Poincare’s work.
By the same token, Einstein used non-Euclidean geometry to formulate the General Theory of Relativity, but he did not discover non-Euclidean geometry. That was done earlier by mathematicians.
Physical dynamics can be chaotic, but chaos is not part of dynamics. Chaos is math. Same for calculus.
There are many systems regarded as chaotic – including the Earth system. That is ice, cloud, wind, fire and water.
At the end, power law based PDFs can also be called self organized criticality. As you point out, lots of phenomenon follow this characteristic behavior. Does climate, or elements of climate exhibit self organized criticality like behavior?
This favorite of mine in climate and modelling is now nearly 10 yeas old. It suggests that model uncertainty is substantial at seasonal to decadal scales. To solve that will require thousandths of times more computer capacity needing energy input of six medium sized cities – it will need modular nuclear energy – and a heat sink the size of Texas. A trillion dollars – cheap at half the price. This would output fine scale seasonal to decadal forecasts with nested process scales in a real world validated model.
https://watertechbyrie.files.wordpress.com/2014/06/hurrell.png
“There is a new perspective of a continuum of prediction problems, with a blurring of the distinction between short-term predictions and long-term climate projections. At the heart of this new perspective is the realization that all climate system predictions, regardless of time scale, share common processes and mechanisms; moreover, interactions across time and space scales are fundamental to the climate system itself. Further, just as seasonal-to-interannual predictions start from an estimate of the state of the climate system, there is a growing realization that decadal and longer-term climate predictions could be initialized with estimates of the current observed state of the atmosphere, oceans, cryosphere, and land surface. Even though the prediction problem itself is seamless, the best practical approach to it may be described as unified: models aimed at different time scales and phenomena may have large commonality but place emphasis on different aspects of the system. The potential benefits of this commonality are significant and include improved predictions on all time scales and stronger collaboration and shared knowledge, infrastructure, and technical capabilities among those in the weather and climate prediction communities.”
https://journals.ametsoc.org/doi/10.1175/2009BAMS2752.1
And then multidecadal climate shifts shift again and all bets are off. Predictability becomes 50/50. A toss of a coin. Due anytime in about 10 years – if it is not happening now? Does the greenhouse gas wedge bias the Earth system magnetic pendulum simulator to warmer states? Perhaps. But can we predict that better than a coin toss? Perhaps not.
“However, we are still miles away from any reliable answers to the question whether the coming winter in Germany will be rather warm or cold”. Prof. Latif cautions against too much optimism regarding short-term regional climate predictions: “Since the reliability of those predictions is still at about 50%, you might as well flip a coin.”
https://www.geomar.de/en/news/article/klimavorhersagen-ueber-mehrere-jahre-moeglich/
David
I am a bit puzzled by this talk of temporal versus spatio-temporal chaos. What bothers me is that chaos is a mathematical property and as such it is neither temporal, spatial or spatio-temporal. Chaos is a property of certain equations, or sets of equations, and these are not in themselves about anything, much less about things in space and time.
This is an excellent comment and one that must be answered .
Be very sure that you are not alone and there are some people commenting here who are not only puzzled but clearly are not getting it at all .
Imagine that you meet somebody and he says “Mechanics is mechanics so what’s this fuss with quantum mechanics ? There should be no difference between classical and quantum mechanics .”
So you say “Well, the fundamental difference is that classical mechanics solutions are real valued while the solutions of the Schrödinger equations are complex valued . This mathematical difference leads to very different physics.”
If the person then says “Numbers are numbers so there is no reason that quantum and classical mechanics be different .” then you can stop any discussion because it’d be just a waste of time . This person is obviously mathematically illiterate and will never get quantum mechanics .
Actually differences between temporal chaos and spatio-temporal chaos are bigger than differences between classical mechanics and quantum mechanics .
So I will make a list of differences between temporal chaos and spatio-temporal chaos .
You can then test yourself . If you understand what these differences mean and why they lead to different physics then you just need to update your knowledge and you may get it . If you don’t understand the differences then you have either a few years of studies to do or you won’t get it .
1)
– The dynamics of temporally chaotic systems are governed by a finite number of non linear ODE
– The dynamics of spatio-temporally chaotic systems are governed by non-linear PDE
2)
– The phase space in temporal chaos is finite dimensional and isomorphe to R^n . If n=2 or 3 , it can be represented like the usual everyday space
– The phase space in spatio-temporal chaos is the infinite dimensional space of functions .
3)
– a point in the phase space of temporal chaos is a “normal” point in R^n
– a point in the phase space of spatio-temporal chaos is a function
4)
-An orbit in the phase space of temporal chaos is a usual parametric curve
– An orbit in the phase space of spatio temporal chaos is a set of functions
5)
– It is easy to find a finite orthonormal basis in the phase space of temporal chaos
– there is no finite orthonormal basis in spatio-temporal chaos
6)
– The norm in the phase space of temporal chaos is the usual euclidean norm
– There are many possible norms with different properties in the phase space of spatio-temporal chaos . This issue is both quite difficult and very important .
7)
– An attractor in temporal chaos is an invariant set of points but has a non integer dimension . A Strange attractor is a fractal .
– An attractor in spatio temporal chaos is a set of functions, generally infinite dimensional .
8)
– It is easy to find compact sets (so the topology is easy) in temporal chaos
– There are no compact sets in the infinite dimensional function space of spatio-temporal chaos .
We can stop here but the list goes farther and gets increasingly difficult .
Thanks Tomas. But we may have to eyeball it in, I was down the beach yesterday with sun, wind, cloud and waves. It may be yet more chaotic in a physical system.
Well Robert, chaos in maths and in physics is basically the same thing, different perspective .
While mathematics is not all physics, physics without mathematics would be just an incomplete list of random mysterious partly contradictory rules and commandments .
It would be a religion but not a science .
Hi Tomas
Perhaps more like a detective story or a forensic investigation. The abjuctive method of science. Less precise but heaps of fun in hydrology, biology, physiology. economics…
Watch it – there’s an elephant in the room.
Bye (:
Thanks Tomas. That is a long list of differences, so what are the similarities, such that they are both chaos? Are they both about aperiodic oscillators?
I would say there are 4 fundamental similarities :
unpredictability, pseudo-randomness, irreversibility and the concept of an attractor even if the attractor is mathematically very different for the 2 cases .
Physically it is necessary to have an energy dissipation process . You need energy to make things move and dissipation to make them stop . So in a way those 2 processes work against each other and when they interact in a specific non linear way they “don’t know” if they should move or stop and fluctuate between both tendencies . This is just an image – not saying that it is exactly so that it happens but it is not far . This issue is cutting edge research – it is still not known whether there is a unique road to chaos or if there are several qualitatively different roads .
The Hamiltonian chaos discovered by Poincaré that I mentionned above is again Something else because there is no dissipation . Some people actually consider that it is not a “standard” chaos even if it shares some features .
Actually thinking about it, you may be right – I am not sure if using the same word “chaos” for all these processes is a good idea for non experts because it seems to imply that there is a single underlying physical (or mathematical) process explaining all the different cases but it is not sure at all that it is so .
But use has consecrated the word so that people who study non linear dynamics know that a logistic map is not the same as turbulence which is not the same as the N body problem even if they use the same word “chaos” .
My point about Poincare is that chaos math and chaos dynamics are two different things. Dynamics is applied math but there is also pure math. It is likely that Newton was looking at physical mechanics when he invented (or some say discovered) calculus. But that does not make calculus part of physics.
But the fundamental properties of chaos are mathematical properties. They are not about or based on any particular physical situation.
This is why chaos was discovered by a mathematician, Poincare, not a physicist.
Oh !
This is backwards . Poincaré was before everything else a great physicist .
It is said that he was the last of the physicists who were as skilled in mathematics as in physics .
He wrote a seminal book (La science et l’hypothèse”) about the “unimportance” of absolute time, space and ether , completed the Lorentz transformations and showed that they leave Maxwell equations invariant what is basis of special relativity well before Einstein .
He made a mistake to consider that the space and time contraction/dilatation were physical while Einstein considered that they were a perspective effect in a 4D space-time .
Paradoxally Einstein’s argument was mathematical while Poincare’s was physical and it was Einstein who was right and That’s why he’s the father of relativity and not Poincaré .
If it is true that he was the first to find chaotic dynamics (even if he didn’t use this word) it came from a pure physical study of the mechanical 3 body problem .
It was actually the other way round – the chaos preexisted in physics where Poincare diiscovered it and it was only later that he developped the mathematics to deal with it .
(Note : this kind of chaos in mechanical systems like the N body problem is a special Hamiltonian chaos and it has for consequence that orbits in an N body system are unstable and not predictable even if stable configurations may coexist with unstable ones)
What happens, does happen, it is not chaos.
When what happens is not understood, it is considered chaos.
In a true chaotic universe, earth would not have survived.
Natural events happen for actual real reasons. Us not understanding the reasons does not make it chaos.
What happens, does happen, it is not chaos.
When what happens is not understood, it is considered chaos.
In a true chaotic universe, earth would not have survived.
Natural events happen for actual real reasons. Us not understanding the reasons does not make it chaos.
This sounds very much like the example I gave of somebody saying “Mechanics is mechanics so what’s this fuss with quantum mechanics ?”
What’s for you a “true” chaotic Universe and how would you recognize it if you saw it, especially since you say that you don’t understand what happens ?
Be very sure that if you feel like being part of the “us” who don’t understand something, this is far from being the case for everybody .
More generally probably since humanity was able to ask questions, there has always been a boundary where knowledge was uncertain and a very small minority of people who always finished to push this boundary a bit farther .
It still works today as it did 2000 years ago .
ST chaos turns out to be a nice small field, turning out about 600 papers a year. Google Scholar gives about 1000 for 2017-21018. The term spatiotemporal is preferred to spatio-temporal 4 to 1. See
https://scholar.google.com/scholar?as_ylo=2017&q=%22spatiotemporal+chaos%22+OR+%22spatio-temporal+chaos%22&hl=en&as_sdt=1,49
My earlier conjecture looks to be about right. Some (or all) 2D and 3D temporal (that is, ordinary) chaotic cases exhibit interesting spatial patterns, the study of which is spatiotemporal chaos. This structural analysis is necessarily far more complex than ordinary temporal chaos, which just considers the state of the system as a point in state space. ST chaos is unpacking the state and how it is changing.
On a quick look it appears that it is the chaotic time evolution of these patterns that is studied, although the spatial structure at a given time might also be chaotic. Interestingly, I can find no nontechnical exposition of spatiotemporal chaos, other than a few websites like these:
http://www.mcc.caltech.edu/st_chaos.html
http://www.ds.mpg.de/LFPB/chaos
Given that ST chaos is looking at things like heart attacks, they could use some popular science. They also seem to be doing a far bit of weather and climate research.
Reblogged this on I Didn't Ask To Be a Blog.
Joni Mitchel nailed this in 1969 ;
Pingback: Weekly Climate and Energy News Roundup #320 |
The Radiative Greenhouse Effect Theory
Premise 1:
The earth is 33 C warmer with an atmosphere than without. (288 K – 255 K = 33 K)
So, just how does that work?
Premise 2:
There is an up/down/”back” radiative CO2/GHG energy loop between the surface and the atmosphere that “traps” and recirculates energy through QED processes warming both the atmosphere and the surface.
And what powers that energy loop?
Premise 3:
The surface radiates as a 288 K black body with an emission of 390 W/m^2 (K-T 289 K & 396 W/m^2)
Premise 1, 2 & 3 are demonstrably false.
No 33 C warmer + No up/down/”back” radiation loop + No BB radiation = Carbon dioxide and mankind play ZERO role in the behavior of the climate.
Premise 1:
http://writerbeat.com/articles/15582-To-be-33C-or-not-to-be-33C
Premise 2:
http://writerbeat.com/articles/14306-Greenhouse—We-don-t-need-no-stinkin-greenhouse-Warning-science-ahead-
Premise 3:
http://www.writerbeat.com/articles/21036-S-B-amp-GHG-amp-LWIR-amp-RGHE-amp-CAGW
https://www.linkedin.com/feed/update/urn:li:activity:6394226874976919552